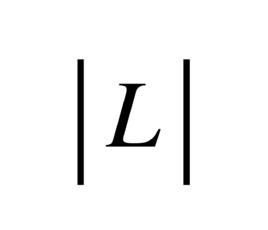簡介
線性系是代數簇上的一族線性等價的有效除子,它為射影空間所參數化。
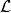 線性系
線性系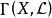 線性系
線性系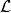 線性系
線性系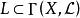 線性系
線性系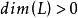 線性系
線性系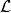 線性系
線性系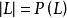 線性系
線性系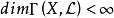 線性系
線性系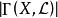 線性系
線性系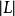 線性系
線性系設 X 是域 k 上非奇異代數簇, 是 X 上的可逆層, 是 的整體截面的空間, 是一個有限維子空間,如果 ,則由 的截面零點所確定的除子是線性等價的有效除子。L 的一維子空間構成的射影空間 就是一個線性系,它給出了上述除子的參數化。如果 ,則稱線性系 為完全的(complete),同樣記為 。
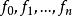 線性系
線性系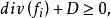 線性系
線性系用除子的語言可以等價地描述為:若 D 是 X 的一個除子, 是 X 上的有理函式,滿足 則稱除子集合
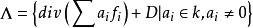 線性系
線性系 線性系
線性系 線性系
線性系為線性系。若 包含所有與 D 線性等價的有效除子,則稱 是 D 的完全線性系。
 線性系
線性系設 是 L 的一個基,通過
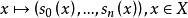 線性系
線性系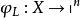 線性系
線性系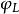 線性系
線性系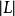 線性系
線性系可定義一個有理映射 。通常就說 由線性系 定義的。
固定分支
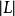 線性系
線性系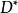 線性系
線性系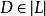 線性系
線性系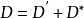 線性系
線性系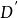 線性系
線性系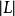 線性系
線性系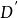 線性系
線性系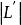 線性系
線性系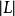 線性系
線性系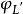 線性系
線性系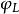 線性系
線性系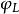 線性系
線性系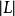 線性系
線性系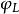 線性系
線性系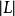 線性系
線性系對於 ,線性系的固定分支(fixed component of a linear system)是指 X 上的一個有效除子 ,使得對任何 都有 ,其中 是一個有效除子。當除子 D 取遍 時,除子 構成一個線性系 ,它與 有相同維數。映射 與 是重合的。所以當考慮 時可以假設 沒有固定分支。在這種情形, 恰在 的基本集上沒有定義。
舉例
比如D和除子E線性等價,D=div(s), E=div(t), 那么 f=s/t 恰好是個半純函式。
D的一個線性系, 就是指和D線性等價的一些 有效除子 構成的集合, 並且這些有效除子對應的截面全體恰好構成一個線性空間。D有很多線性系,其中有一個最大的線性系, 記為|D|, 它包含了其他任何一個線性系, 我們稱這個線性係為D的完全線性系。換句話說,|D|的所有元素對應的截面恰好構成了最大的線性空間。
有的時候,人們也把線性系中的有效除子直接用截面來替代,這樣我們就可以把線性系直接看成這些截面張成的線性子空間。 由此我們可以定義X到射影空間的映射。
比如|D|是由截面 s,s,...,s張成的線性系。於是可定義映射(其中P 是射影空間, [...]是射影齊次坐標):Φ: X→P , x→[s(x), s(x),...,s(x)]。有趣的是,這個映射和選取的基 s,s,...,s無關。 當然Φ在某些點上可能沒有定義,所以我們稱Φ為有理映射。
上面是用完全線性系定義的,也可用其他的線性系定義。反過來, 任何有理映射都是某個除子D的線性系定義的類似上述的映射。這樣,研究除子就有了很重要的幾何意義。