定義
線性空間V到自身的映射通常稱為V上的一個變換。
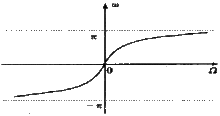 線性變換參考圖
線性變換參考圖同時具有以下定義:
線性空間V上的一個變換A稱為線性變換,如果對於V中任意的元素α,β和數域P中任意k,都有
A(α+β)=A(α)+A(β)
A (kα)=kA(α)
線性代數研究的一個對象,即向量空間到自身的保運算的映射。例如,對任意線性空間V,位似是V上的線性變換,平移則不是V上的線性變換。對線性變換的討論可藉助矩陣實現。σ關於不同基的矩陣是相似的。Kerσ={a∈V|σ(a)=θ}(式中θ指零向量)稱為σ的核,Imσ={σ(a)|a∈V}稱為σ的象,是刻畫σ的兩個重要概念。
對於歐幾里得空間,若σ關於標準正交基的矩陣是正交(對稱)矩陣,則稱σ為正交(對稱)變換。正交變換具有保內積、保長、保角等性質,對稱變換具有性質:〈σ(a),β〉=〈a,σ(
 線性變換
線性變換在數學中,線性映射(也叫做線性變換或線性運算元)是在兩個向量空間之間的函式,它保持向量加法和標量乘法的運算。術語“線性變換”特別常用,尤其是對從向量空間到自身的線性映射(自同態)。
在抽象代數中,線性映射是向量空間的同態,或在給定的域上的向量空間所構成的範疇中的態射。
理解
關於線性變換和特徵值的理解
 線性變換參考圖
線性變換參考圖首先我們來看這樣一個事實。一個二維的直角坐標系XOY,然後逆時針方向鏇轉了ө角變為X’OY’後,那么我們考察一下後會發現,在XOY和 X’OY’的坐標系之間存在這樣的轉化關係。這裡我們進一步來理解這個等式的含義。就是說在XOY坐標系下的某一個點 在X’OY’坐標系下的坐標變為了 。那么我們同樣來考察一下這兩個坐標系下的基坐標。就是來考察在XOY坐標系下的基坐標 (1,0)和 (0,1)在新的坐標系X’OY’下的 基坐標下的投影大小用 (1,0)和 (0,1)來表示為這樣的。 (1,0)在 的投影 = ; (1,0)在 的投影 = ;。那么我們就說這個坐標鏇轉線性變換的變換矩陣為 。注意,這裡的矩陣的排列是前面兩個基坐標係數方程的轉置矩陣,之所以寫為轉置矩陣是因為我們習慣這樣來寫基坐標的線性變換A =( , ) 。我們可以看到這樣的鏇轉變換的目的就是把坐標系鏇轉後來看一下。這樣的鏇轉角度一旦確定以後,我們就能夠得到原來的老坐標下的坐標點在新坐標系下的坐標為 。注意的是,這裡的坐標是右乘變換矩陣。我們指出(從後面可以進一步清楚地理解,這裡的鏇轉變換隻不過是線性變換的一個具體的例子而已。更廣義的線性變換的例子我們將在下面進一步理解)。下面我們來理解什麼是線性變換。它的數學定義在一般的高等代數學書中都可以找到。A(a+b)=Aa+Ab,Aka=kAa。其中a,b是V中的線性空間(線性空間的定義還是繼續看高等代數書吧)。這個定義就是說把空間中的元素(特殊地想為三維空間的向量)經過一個變換,而這種變換是具有線性的特性的(就是滿足上面的那個和、乘關係。三維空間的一個坐標鏇轉就滿這種關係,可見,所謂的線性變換隻不過是一個很抽象的一類具體變換的集合,很多例子)。
那么這種變換的從一個元素轉變到另外一個元素的對應關係,我們可以用前面的一個矩陣來表示,稱為線性變換矩陣。這個的意義就是給出從一個元素變化到另外一個元素的轉換關係而已,這樣來看的話,那么前面的坐標系鏇轉只不過是線性變換的一個具體例子而已。線性變換的生動例子太廣了。為了後面的說明的需要,我們來仔細考察下面的一個很有意思的例子。在三維空間中,我們有一個球心在原點(XOYZ和 X’OY’Z’的坐標系具有不為零的三個歐拉角)的球面,球面上的每一個點當然都有一個空間矢量,現在呢,我們讓這個球開始沿著X’OY’Z’的三個主軸方向變化,假設X’,Z’方向膨脹,Y’方向收縮,那么我們可以想見,只有這三個方向的位置矢量是沿著原來的方向變化著的,其它的位置矢量在新的位置都會和原來的位置矢量有一個夾角。容易直觀的理解,這樣的變換是線性變換,下面我們要考慮的問題是,怎樣來描述這樣一個變換過程。無疑我們可以用變換矩陣來表明表面上任意一個點在變化前後的位置對應關係。但是,我們似乎可以預計,如果用X’OY’Z’坐標系(一個基坐標)來描述這種變換的話,要比XOYZ坐標系(另外一個基坐標)下的變換矩陣要簡單一些。呵呵,問題是,在一般情況下,我們得到的變換矩陣都是在一般的基坐標下的矩陣,怎樣找到這個特殊的基坐標呢,自然也是我們的問題之所在了。好了,有了這個基礎理解,下面我們來點理論的事情。前面的二維例子已經指出,變換矩陣就是把一個元素(向量)變換到另外一個元素(向量)的過程。那么,我們先來考察這個元素是基坐標的特列會得到什麼樣的結果。假設我們已經給出這樣的一個變換矩陣。 那么我們再來右乘一個基坐標 變為 (注意,矩陣的這種乘法就相當於張量右向點乘一個矢量)。得到的結果就是這個基向量 = 變為了 = 。
變為了一個不和原來的基坐標同方向的矢量。同樣地,其它兩個基坐標也會變化為其它的方向。進一步我們指出,如果說空間中的向量(因為任何一個向量都可以用無關的基向量表述,所以我們可以自然拓廣為包含基坐標的一般向量)在這個變換下得到的變換後的坐標與原來的關係為: = 。我們可以想像,在這種變換矩陣的作用下,能否找到空間中某一個向量經過這種方式變換以後,具有和原來的向量同方向,但是只是它的這個大小具有 倍的關係,即我們經常見到的 。假設我們這樣的向量 存在的話,那么我們的 就稱為特徵向量,(因為其具有線性變換下方向不變的特徵), 稱為特徵值。很顯然,我們可以用前面的圓球變橢球來想像,這種情況是可能發生的,但是,我們指出,這種情況發生與否只與變換矩陣本身相關。關於變換矩陣的特徵值和特徵向量我們多說一句,其具體的求法就是求解一個特徵多項式,得到特徵值後,將每一個特徵值反帶回元原來的方程組得到特徵向量。並且,我們指出,物理意義上相同的同一個線性變換,用不同的基坐標來表示得到的變換矩陣是不一樣的(就拿鏇轉變換來說吧,假設我現在已經有了兩個坐標系XOY和 X’OY’,現在又有第三個坐標X’’OY’’首先與XOY重合,然後在鏇轉一個角度,那么這個轉轉變換在XOY和 X’OY’坐標系下的變換矩陣顯然是不一樣的,因為針對不同坐標系的鏇轉角度是不一樣的)。但是,可以證明同一種變換在不同的基坐標下的變換矩陣是相似的。並且可以證明相似矩陣具有相同的特徵多項式,這也就是說同一個變換的特徵多項式至於變換本身有關係,而與具體的選擇的基坐標無關,是有變換本身的特性決定的。
那么,我們自然可以相問,能否找到一個基,使得這個變換矩陣具有最簡單的形式(當然是對角矩陣了)。換句話說,就是能否找到一個矩陣和對角性矩陣相似。如果可以的話,那么這個對角形矩陣是由什麼組成的,。下面,我們先來在假設第一個問題量是肯定的情況下,來看看第二個問題。我們還是用前面的圓球變橢球來想像,這種物理上的變換是不會隨著基坐標系的改變而改變的。那么就圓球變橢球的例子,我們可以看到,在XOY坐標系下的變換矩陣不簡單,但是,如果我們將基坐標選擇為和 X’OY’重合,那么在這個坐標系下,同樣基坐標方向上的那個向量在進行矩陣變換後只是變為原來的λ倍。由 = ,同樣的,我們換用其它的兩個基 = ; = 。可以看出,要實現這樣的變化只能是 = = = = = =0,而 , , 。這樣的話,在這個特徵向量作為基的情況下,我們得到的線性變換的矩陣是最簡單的對角形矩陣,並且對角線上的元素全是特徵向量的特徵值,至於具體的排列順序沒有嚴格的要求,但是,必須和你選擇的基坐標的順序一樣,也就是說,如果選擇 位置的話,那么就同時必須把 對應的特徵向量作為X方向的基坐標。
同時我們也可以看到,在三維空間中,變換矩陣表示為對角形的三個基向量是線性無關的,這個概念推廣就是我們一般的結論那就是一個nxn維變換矩陣能相識於一個對角形矩陣(或者說可以在特徵向量的基坐標下變化為對角形)的充要條件就是必須必須具有n個線性無關的特徵向量。如果這一結論對多有矩陣都成立的話就比較完美了,但是可惜的是,並非所有矩陣都有和其維數一樣多的特徵向量。但是,我們可以得出如下的結論。1、屬於不同特徵值的特徵向量彼此之間線性無關,2、如果某一特徵值有幾個線性無關向的特徵向量,那么這幾個線性無關向量和其它任何不同特徵值的特徵向量是線性無關的。3、矩陣相似與對角陣的條件是矩陣有和維數一樣多的線性無關特徵向量。好了,問題基本就解決了,我們最後指出,實對稱矩陣必定可以對角化。最後我們來聯繫流體力學來看,張量的意思就是把變化到另外一個地方去。那么變形速度張量和一個的右向內積就是得到一個變形速度。
正文
同一域上兩個向量空間之間的映射,是線性代數的一個主要研究對象。
設V和V┡是域 K上的向量空間,L是從V到V┡的映射,如果對於V中任意向量 u、v以及K中任意元素α、b,有L(αu+bv)=αL(u)+b)L(v),那么L 稱為V到V┡的線性變換。例如,解析幾何里的三維空間中任一向量(尣,y,z)在xy平面上的投影:L((尣,y,z))=(尣,y),就是實數域R上三維向量空間R到二維向量空間R的一個線性變換。設尣是n維向量,M是m×n實矩陣,令L(尣)=M·尣,則L就是R到R的一個線性變換。
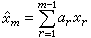 線性變換
線性變換設L 是V 到V┡的一個線性變換, B ={b)j|j=1,2,…,n}和 C ={сj|i=1,2,…,m}分別是 V 和V┡的基,於是,V 中任一元素尣可表為
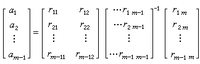 線性變換
線性變換,其中xj是域K的元素。由線性變換的定義可推得
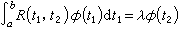 線性變換
線性變換。若
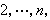 線性變換
線性變換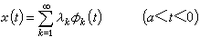 線性變換
線性變換式中αij是域 K 的元素,令M(L)=(αij),尣寫為列向量(x1,x2,…xn),則L(尣)=M(L)·尣。此時M(L)稱為L對(B,C)基的矩陣。當基取定之後,就在L與M(L)之間建立了一一對應關係,即V到V的一切線性變換與K上一切n×m 矩陣之間是一一對應的。線性變換保持子空間及其包含關係,即若S1、S2都是V的子空間,且有
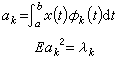 線性變換
線性變換時,則L(S1)、L(S2)必是V┡的子空間,且有
。V┡的零向量在V中的原像組成的集合,稱為L的核,記作KerL,L(V)表示V在L作用下的像,則KerL和L(V)分別為V和V┡的子空間,若以dim KerL 和dimL(V)分別表示子空間KerL 和L(V)的維數,則有dimKerL+dimL(V)=dimV。dim KerL稱為L的虧,dimL(V)稱為L的秩。
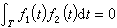 線性變換
線性變換從線性變換和矩陣的對應關係可知這兩者是同一的,但是線性變換的矩陣與基有關,而線性變換卻不受基的限制,所以線性變換使用起來要方便一些。例如,解齊次線性方程組:
就可看作求KerL的問題,這裡L是矩陣(αij)所代表的線性變換。因此,當L的虧為0時方程組只有零解。在m
在V=V┡時,若V 到V┡的線性變換L是一個雙射,則L 稱為可逆變換或非奇異變換。從虧和秩的關係可知以下條件是等價的:①L是正則的;②M(L)是非奇異的;③L(V)=V;④KerV ={o}。V 的正則變換以映射的合成為運算構成一個群,稱為V上的一般線性群,記作GL(V)。
在V和V┡都是賦范線性空間時,V到V┡的線性變換就稱為線性運算元。如果V┡是一維實空間,那么就把線性運算元稱為線性泛函。對於線性運算元L若存在常數M,使得‖L(尣)‖≤M·‖尣‖,對於V的一切x都成立,那么L稱為有界的。對於線性運算元來說,有界和一致連續是等價的。

