背景
1911 年秋天，在布魯塞爾召開的第一次索爾維會議上，洛倫茲（Hendrik Lorentz）提出了一個問題：如果鐘擺的擺線長度逐漸減小，那么這個鐘擺的擺動會怎樣變化呢？愛因斯坦（Albert Einstein）答道：如果擺線的長度以極慢的速度減小，那么鐘擺的能量會從 hv' 變成 hv（意思是鐘擺的頻率和能量都在變，但是二者的比值 h 恆定）。 愛因斯坦的想法可算是絕熱近似的雛形：當某個變數以足夠慢的速度變化時，體系的某個屬性是不發生變化的。
1916 年，保羅·埃倫費斯特（Paul Ehrenfest）提出了絕熱不變數（又稱浸漸不變數）的概念。當一參數發生某種緩慢變化時，物理體系的某個屬性保持恆定，這個屬性就是絕熱不變數。 許多物理學家和數學家都嘗試過用絕熱不變數來解答洛倫茲的鐘擺問題，他們在解答過程中既運用了經典力學原理，又運用了量子力學原理。 可以說，絕熱不變數是連通巨觀世界和微觀世界的橋樑之一。
1928 年，麥克斯·玻恩（Max Born）和弗拉基米爾·福克（Vladimir Fock）基於埃倫費斯特的研究和微擾理論，正式提出了絕熱近似的理論。兩人證明了在微擾的變化速度極其緩慢時，哈密爾頓量逐漸變化而不是呈跳躍性變化，儘管哈密爾頓量的初始值和最終值不同，但初始值的本徵態和最終值的本徵態是同一數值。
證明過程
含時的薛丁格方程寫作：
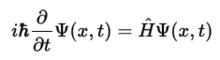絕熱近似它的一般解是：
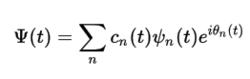絕熱近似其中
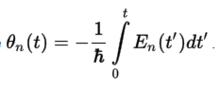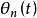絕熱近似
絕熱近似相被稱為動力相因子。代入薛丁格方程，可得：
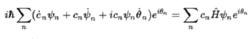絕熱近似其中等號左邊第三項和等號右邊部分相等，消去後，得：
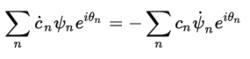絕熱近似由於在任意時刻，有：
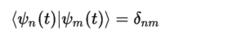絕熱近似則
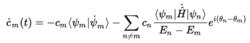絕熱近似由於在絕熱近似中，哈密爾頓量的時間導數極小，最後一項省略，展開可得：
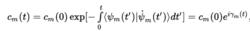絕熱近似由於
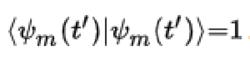絕熱近似整理可得：
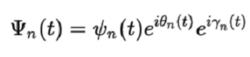絕熱近似因此，在絕熱近似中，一個體系如果一開始在第 n 本徵態，則在哈密爾頓量變化之後還是在第 n 本徵態。
Berry 相
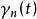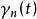絕熱近似 絕熱近似上述最後一個公式中，被稱為幾何相因子。在某些絕熱近似的過程中，幾何相因子可以被消去。然而，當絕熱演化是循環過程的時候，就是規範不變的物理量了，稱為 Berry 相 （Berry phase）。
當一個鐘擺在北極點擺動時，由於不受地球自轉的影響，擺動平面相對於地球是不動的。如果把這個鐘擺緩慢移動到赤道，再沿赤道緩慢移動幾公里，最後沿著緯線緩慢移動回到北極點，那么此時它的擺動平面和一開始相比，就有了一個偏轉角。儘管在這個過程中，鐘擺的其它性質沒變，擺動平面相對於地球的角度卻變了。
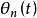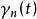絕熱近似 絕熱近似在量子力學中，有和這個巨觀物理模型相似的情況。在絕熱近似中，本徵態沒有發生變化並不意味著相沒有發生變化。相包含兩個方面，一個是上述公式中的，即動力相，另一個是，即幾何相。把含時薛丁格方程
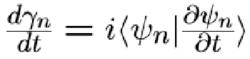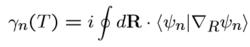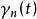絕熱近似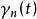
絕熱近似 絕熱近似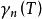 絕熱近似
絕熱近似對時間積分，就可得到的解。是由哈密爾頓量里的一系列變數決定的。假設在一個循環過程中，經過時間 T 後，所有這些變數都回到初始值，那么我們把這些變數對時間積分，可得：其中 R 代表這一系列變數。這個就是 Berry 相。整個推導過程的基本假設是絕熱近似。
