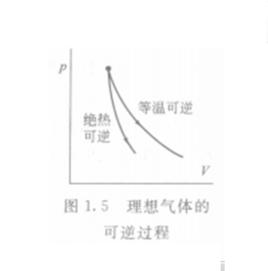
簡介
絕熱過程
絕熱過程就是在狀態變化過程中，系統與環境之間沒有熱交換的過程。實際上真正的絕熱過程是不存在的，但是可以把在隔熱性能較好的密閉容器內發生的狀態變化過程近似看作絕熱過程。有時雖然容器的絕熱性能不是很好，但是其中的狀態變化過程或化學反應在很短的時間內就能完成，在此期間由於時間短，系統與環境交換的熱量很少，必要時也可以把這種過程近似看作絕熱過程。
基本公式
對於封閉系統絕熱過程，因Q=0，則由熱力學第一定律數學表達式可得：
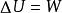絕熱可逆過程無論絕熱過程是否可逆，上式均可成立。對於純理想氣體封閉系統的絕熱過程，則由上式得：
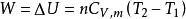絕熱可逆過程上式表明，在絕熱過程中，系統對外做功（如絕熱膨脹），需要消耗系統的熱力學能，系統溫度必然降低；系統得到功（如絕熱壓縮），將使系統的熱力學能增加，系統溫度必然升高。
可逆絕熱過程方程
使用條件
（1）理想氣體封閉系統；
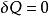絕熱可逆過程（2）；
（3）可逆；
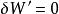絕熱可逆過程（4）。
具體方程式
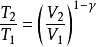絕熱可逆過程
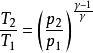絕熱可逆過程
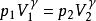絕熱可逆過程其中：
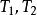絕熱可逆過程（1） 表示系統始、終態的溫度，K；
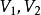絕熱可逆過程
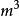絕熱可逆過程（2） 表示系統始、終態的體積， ；
絕熱可逆過程（3） 表示系統始、終態的壓力，Pa；
絕熱可逆過程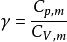
絕熱可逆過程（4） 表示絕熱指數或熱容商， 。
功能
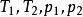絕熱可逆過程
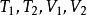絕熱可逆過程
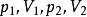絕熱可逆過程
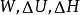絕熱可逆過程在理想氣體的可逆絕熱過程中，若已知或或中任意三個量，利用上述方程式，就可以求第四個量，進而可以求得。
典例
例1
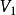絕熱可逆過程
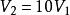絕熱可逆過程2.0mol理想氣體從始態202.65kPa、恆溫可逆膨脹到，對外做功41.85kJ，求系統的溫度和始態體積。
解：根據
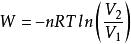絕熱可逆過程
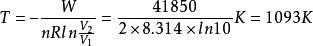絕熱可逆過程
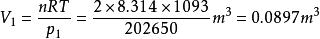絕熱可逆過程 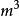絕熱可逆過程最終得系統的溫度和始態體積分別為1093K和0.0897。
例2
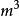絕熱可逆過程某理想氣體2.00mol從始態298K、200kPa，恆溫可逆膨脹到0.100，求過程的功。
解：對理想氣體恆溫可逆膨脹過程
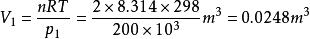絕熱可逆過程
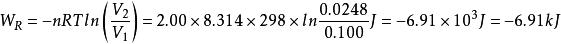絕熱可逆過程故此理想氣體在該恆溫可逆膨脹過程中，對環境做功6.91kJ。
例3
1.00mol單原子理想氣體在298K、1.00×10^3kPa下可逆絕熱膨脹到終態，壓力為100kPa，求算終態體積、終態溫度及所做的功、△U和△H。
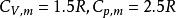絕熱可逆過程解：已知單原子理想氣體的，故
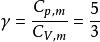絕熱可逆過程則
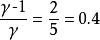絕熱可逆過程根據可逆絕熱過程的方程可求得終態溫度
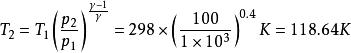絕熱可逆過程
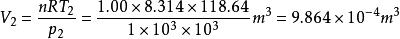絕熱可逆過程故有：
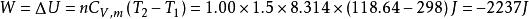絕熱可逆過程
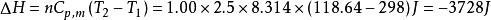絕熱可逆過程