金融風險測度理論

金融風險測度理論（FinancialRiskMeasurement）金融風險管理是各類金融機構所從事的全部業務和管理活動中最核心的內容，它和時間價值、資產定價被並稱為是現代金融理論的三大支柱。金融風險管理分為識別風險、測量風險、處理風險以及風險管理的評估和調整四個步驟。其中，金融風險的測量是金融市場風險管理的核心環節。風險測量的質量，很大程度上決定了金融市場風險管理的有效性；合理風險測度指標的選取，是提高風險測量質量的有效保障。

理論工作

風險管理的基礎工作是度量風險，而選擇合適的風險度量指標和科學的計算方法是正確度量風險的基礎，也是建立一個有效風險管理體系的前提。風險測度就是各種風險度量指標的總稱。

風險測度理論的發展大致經歷了三個階段：首先是以方差和風險因子等為主要度量指標的傳統風險測度階段；其次是以現行國際標準風險測度工具VaR為代表的現代風險測度階段；最後是以ES為代表的一致性風險測度階段。

傳統風險

金融風險測度理論

傳統風險測度工具包括方差、半（下）方差、下偏矩LPM（LowPartialMoments）、久期（duration）、凸性（convexity）、beta、delta、gamma、theta、vega、rho等，這些指標分別從不同的角度反映了投資價值對風險因子的敏感程度，因此被統稱為風險敏感性度量指標。風險敏感性度量指標只能在一定程度上反映風險的特徵，難以全面綜合地度量風險，因此只能適用於特定地金融工具或在特定的範圍內使用。

方差、半（下）方差、下偏矩LPM等風險敏感性度量指標只能描述收益的不確定性，即偏離期望收益的程度，並不能確切指明證券組合的損失的大小。所以，它們只是在一定程度上反映風險的特徵，難以全面綜合地度量風險，因此只能適用於特定地金融工具或在特定的範圍內使用。

現代風險

金融風險測度理論

現行的國際標準風險管理工具VaR最初由J.P.Morgan針對其銀行業務風險的需要提出的，並很快被推廣成為了一種產業標準。風險價值VaR是指在正常的市場條件和給定的置信水平下，在給定的持有期間內，投資組合所面臨的潛在最大損失。VaR是藉助機率論和數理統計的方法對金融風險進行量化和測度。它最大的優點是可以得出多維風險的一個一維近似值，可用於測量不同市場的不同風險並用一個數值表示出來，因此具有廣泛的適用性。巴塞爾銀行監督委員會、美國聯邦儲備銀行、美國證券交易委員會、歐盟都接受VaR作為風險度量和風險披露的工具。

但是，VaR作為風險測度的指標，不滿足一致性風險測度四條公理中的次可加性公理，不是一種一致性風險測度指標。這就意味著當用VaR度量風險時，某種投資組合的風險可能會比各組成成分證券風險之和還要大，從而導致投資者不願多樣化投資的情況。而且VaR不能測度超過VaR的損失、不適用於非橢球分布函式族、VaR有許多局部極值導致VaR排序不穩定等缺陷，決定著VaR並不是一種合適的風險測度指標。

基於上述風險測度的局限性，Artzner等（1999年）提出了一致性風險測度（CoherentRiskMeasure）概念。他們認為一種良好定義的風險測度應該滿足單調性、一次齊次性、平移不變性和次可加性四條公理，並將滿足這些公理的風險測度成為一致性風險測度。

單調性：X1≥X2→ρ(X1)≤ρ(X2)

如果投資組合X1在任意情況下的價值都比投資組合X2的價值大，則一致性風險測度度量的X1的風險至少不應該比X2的風險大。也就是說，優質資產的風險應該比劣質資產的風險小。

一次齊次性：

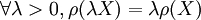金融風險測度理論

平移不變性：

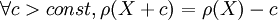金融風險測度理論

即意味著：ρ(X+ρ(X))=ρ(X)−ρ(X)=0

上式意味著，如果用數量為ρ(X)的資本或保證金加入到投資組合X之中，則恰好可以抵消投資組合X的風險。因此，平移不變性公理要求風險測度在數值上就是為抵消投資組合的風險而需要提供的資本或保證金的數量。

次可加性：

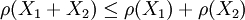金融風險測度理論

次可加性公理意味著，用一致性風險測度度量出來的所有被監管對象的總體風險A，不能比各單個被監管對象的風險之和B大。否則，即使各個被監管對象都設定了足夠的資本或保證金A，也不能保證所有監管對象總的資本或保證金ρ(Xi)足以抵消整體風險B，因此監管措施就可能失效。可見，次可加性公理主要是從保證風險監管有效性的角度提出的，為監管目的而設計的風險測度應該滿足次可加性公理。

其中：

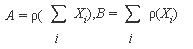金融風險測度理論

由於這四條公理的合理性，一致性風險測度不久就被風險測度理論界廣泛接受。

測度階段

數理金融

數理金融學家隨後在一致性風險測度四公理基礎上提出了幾種形式不同的一致性風險測度指標，其中ES是最常用的一種。ES就是投資組合在給定置信水平決定的左尾機率區間內可能發生的平均損失，因此被成為ExpectedShortfall。ES對於損失X的分布沒有特殊的要求，在分布函式連續和不連續的情況下都能保持一致性風險測度這一性質，使ES不僅可以套用到任何的金融工具的風險測量和風險控制，也可以處理具有任何分布形式的風險源，而且保證了在給定風險量的約束條件下最大化預期收益組合的唯一性。

由於ES風險測度的發展時間不長，ES作為一種一致性風險測度也存在著一定的局限性。VaR與一階傳統隨機占優是一致的，ES風險測度與二階傳統隨機占優是一致的；但是，VaR與二階及二階以上傳統隨機占優不是一致的，ES風險測度與三階及三階以上傳統隨機占優不是一致的，在特定情況下，運用VaR和ES都不能做出正確的投資決策。

理論評價

風險測度理論至今為止仍然是一個有待進一步開發和完善的領域，有許多值得深入研究的課題。由於現有各種風險測度指標均存在一定的局限性，新的風險測度理論和建立在其之上的新的風險測度指標（性能優良、便於計算、合理檢驗）是今後值得深入研究的重點和方向。總之，風險測度在投資組合最佳化中的套用對風險管理實踐有較強的指導意義。