定義
若級數的各項符號正負相間,即形如
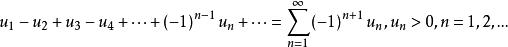 交錯級數
交錯級數的級數叫做交錯級數。
換句話說:交錯級數是正項和負項交替出現的級數。
注意:上式中-1的次數也可以為n,即奇數項為負,偶數項為正。
收斂性判別
萊布尼茨判別法
定理內容
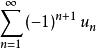 交錯級數
交錯級數如果交錯級數 滿足以下兩個條件:
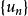 交錯級數
交錯級數(1)數列單調遞減;
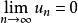 交錯級數
交錯級數(2) ;
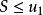 交錯級數
交錯級數那么該交錯級數收斂,且其和滿足。
證明過程
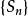 交錯級數
交錯級數考慮交錯級數的部分和數列,它的奇數項和偶數項分別為:
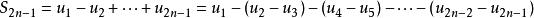 交錯級數
交錯級數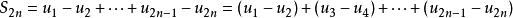 交錯級數
交錯級數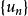 交錯級數
交錯級數∵單調遞減
∴上述二式中括弧內的每一項均為非負數
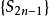 交錯級數
交錯級數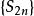 交錯級數
交錯級數∴單調遞減,單調遞增。
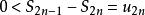 交錯級數
交錯級數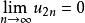 交錯級數
交錯級數∵,且
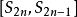 交錯級數
交錯級數∴是一個閉區間套
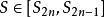 交錯級數
交錯級數由閉區間套定理,存在唯一實數,並且
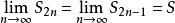 交錯級數
交錯級數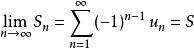 交錯級數
交錯級數∴
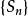 交錯級數
交錯級數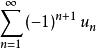 交錯級數
交錯級數故數列收斂,即級數收斂。
適用範圍
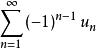 交錯級數
交錯級數注意,萊布尼茨定理所給出的條件(1)是充分非必要條件,即對非單調遞減的數列{u},交錯級數既可能收斂,也可能發散。
換句話說,萊布尼茨定理僅僅給出了判斷交錯級數收斂的充分條件,卻沒有給出判斷交錯級數發散的條件;同時,如果交錯級數滿足該定理的條件,也無法判斷級數是絕對收斂還是條件收斂。
推論(餘項估計)
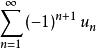 交錯級數
交錯級數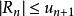 交錯級數
交錯級數如果交錯級數滿足萊布尼茨判別法的兩個條件,則該級數的餘項估計式為:。
典例
例1(交錯調和級數)
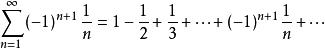 交錯級數
交錯級數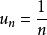 交錯級數
交錯級數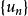 交錯級數
交錯級數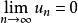 交錯級數
交錯級數知,易得數列單調遞減,且,即該數列滿足萊布尼茨判別法,故交錯調和級數是收斂的。
例2
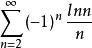 交錯級數
交錯級數判定級數的斂散性。
解:已知該級數是交錯的,我們試圖驗證它滿足萊布尼茨判別法的條件(1)和(2)。
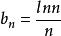 交錯級數
交錯級數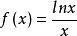 交錯級數
交錯級數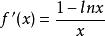 交錯級數
交錯級數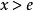 交錯級數
交錯級數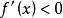 交錯級數
交錯級數 交錯級數
交錯級數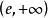 交錯級數
交錯級數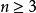 交錯級數
交錯級數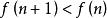 交錯級數
交錯級數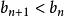 交錯級數
交錯級數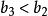 交錯級數
交錯級數數列遞減並不顯然。但是,如果我們考慮與它相應的函式,我們發現。當時,,因此在上遞減,這表明當時,,且,該不等式可直接驗證,故條件(1)滿足。
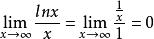 交錯級數
交錯級數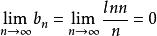 交錯級數
交錯級數條件(2)由洛必達法則易證:,故有,條件(2)滿足。
因此,由萊布尼茨判別法可得,該級數是收斂的。

