相關概念
整數部分是零的小數,稱為純小數.
循環小數是小數位發生循環的小數,依循環開始的數位,可以分為純循環小數和混循環小數兩種。
混循環小數是從十分位後開始循環的小數,如0.1666666666...(1/6),0.009090909....(1/110)等。
特點
(1)分母只含有2或5的因數的最簡分數,可以化為有限小數;
(2)分母中含有2或5以外的因數的最簡分數,可以化為循環小數,但不一定是純循環小數。
(3)若最簡分數a/b的分母b只含有2和5以外的質因數(即b的質因數不包括2和5),則該分數能化為純循環小數。
舉例
實例
1/3=0.33333……是純循環小數
1/5=0.2是有限小數
1/6=0.16666……是混循環小數
例題
求1/2、1/3、……、1/100這99個分數中,有多少個純循環小數?
解:分母中不含2或5這樣的因數的分數,就可以化為純循環小數。
分母含有2的共有100÷2=50個
分母含有5的共有100÷5=20個
分母同時含有2和5的共100÷10=10個
因此不含2和5的有99-50-20+10=39個。
答:99個分數中,有39個可以化為純循環小數。
化成分數
純循環小數化成分數
在國小數學課本中,分數與有限小數是可以互化的。分數可以化成純循環小數,但純循環小數化成分數,並沒有涉及。事實上,兩者也是可以互化的,比起有限小數化成分數,純循環小數化成分數的方法要稍難一些。
例如:有限小數化成分數。
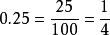 純循環小數
純循環小數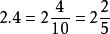 純循環小數
純循環小數只要根據小數的最低位是什麼數位,用10、100、1000等做分母,就可以直接化成分數,不是最簡分數的,要約成最簡分數。
把純循環小數化成分數,並不象有限小數那樣,用10、100、1000等做分母,而要用9、99、999等這樣的數做分母,其中“9”的個數等於一個循環節數字的個數;一個循環節的數字所組成的數,就是這個分數的分子。
例如:
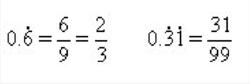 純循環小數
純循環小數混循環小數化成分數
方法描述
一個混循環小數的小數部分可以化成分數:
這個分數的分子是第二個循環節以前的小數部分組成的數與小數部分中不循環部分組成的數的差。
分母的頭幾位數是9,末幾位是0。其中9的個數與循環節中的位數相同,0的個數與不循環部分的位數相同。
舉例
0.13333……化為分數
分子:13-1=12
分母:循環節1位,不循環部分1位,因此是90
即0.13333……=12/90=2/15

