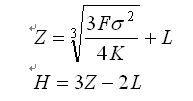基本原理
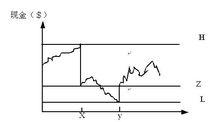米勒-奧爾模型的基本原理右圖說明了米勒-奧爾模型的基本原理。該模型是建立在對控制上限（H）、控制下限（L）以及目標現金餘額（Z）這三者進行分析的基礎之上的。企業的現金餘額在上、下限間隨機波動，在現金餘額處於H和L之間時，不會發生現金交易。當現金餘額升至H時，比如說點X，則企業購入H—Z單位（美元）的有價證券，使現金餘額降至Z。同樣地，當現金餘額降至L，如點Y（下限），企業就需售出Z—L單位有價證券，使現金餘額回升至Z。這兩種情況都是使現金餘額回到Z。其中，下限L的設定是根據企業對現金短缺風險的願意承受程度而確定的。
與鮑摩爾模型相同的是，米勒-奧爾模型也依賴於交易成本和機會成本，且每次轉換有價證券的交易成本被認為是固定的，而每期持有現金的百分比機會成本則是有價證券的日利率。與鮑摩爾模型不同的是，米勒-奧爾模型每期的交易次數是一個隨機變數，且根據每期現金流入與流出量的不同而發生變化。
因此，每期的交易成本就決定於各期有價證券的期望交易次數。同理，持有現金的機會成本就是關於每期期望現金額的函式。
給定企業設定的L，米勒-奧爾模型就可以解出目標現金餘額Z和上限H。現金餘額返回政策的期望總成本等於期望交易成本和期望機會成本之和。米勒和奧爾確定令期望總成本最小的Z（現金返回點）和H（上限）的值為：
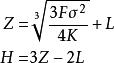米勒-奧爾模型其中：σ 是日淨現金流量的方差。
米勒-奧爾模型中的平均現金餘額為：
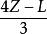米勒-奧爾模型平均現金餘額=
套用意義
要運用米勒-奧爾模型，管理者必須先完成以下四項工作：
（1）設定現金餘額的控制下限。該下限與管理者確定的最低安全邊際有關。
（2）估計日淨現金流量的標準差。
（3）確定利率。
（4）估計轉換有價證券的交易成本。
通過這四步就可以計算出現金餘額的上限和返回點。米勒和奧爾用一個大工業企業九個月的現金餘額數據檢驗了他們的模型。由這一模型得出的日平均現金餘額大大低於企業實際獲得的平均數值。
米勒-奧爾模型更加明確了現金管理的關鍵。首先，該模型說明最優返回點Z*與交易成本F正相關，而與機會成本K負相關。這一發現與鮑摩爾模型的結論是基本一致的。
其次，米勒-奧爾模型說明最優返回點及平均現金餘額都與現金流量這一變數正相關。這就意味著，現金流量更具不確定性的企業應保持更大數額的平均現金餘額。
