簡單介紹
三角形單元適應性強,能適應各種曲折的幾何邊界,但是它的位移函式階次較低,為常應變單元、精度較低,不能反映實際應力的變化情況。而矩形單元的精度高,但適應性差,遇到曲線邊界或非直角的直線邊界難以模擬。雖然可以混合使用兩種單元,但增加了數據準備的工作量。而採用等參數單元,能在同等精度下,可以用較少的單元去求解實際結構。一方面,單元能很好地適應曲線邊界和曲面邊界,準確地模擬結構形狀;另一方面,這種單元要具有較高次的位移模式,能更好地反映結構的複雜應力分布情況,即使單元格線劃分比較稀疏,也可得到較好的計算精度。等參數單元(等參元)就具備了以上兩條優點,因此,得到廣泛套用。
等參數單元(簡稱等參元)就是對單元幾何形狀和單元內的參變數函式採用相同數目的節點參數和相同的形函式進行變換而設計出的一種新型單元。由於等參變換的採用使等參單元的剛度、質量、阻尼、荷載等特性矩陣的計算仍在前面所表示單元的規則域內進行,因此不管各個積分形式的矩陣表示的被積函式如何複雜,仍然可以方便地採用標準化的數值積分方法計算。也正因為如此,等參元已成為有限元法中套用最為廣泛的單元形式。同時,等參單元具有計算精度高和適用性好的特點,是有限元程式中主要採用的單元形式。
基本思想
先將在局部坐標系中簡單幾何形狀的單元,稱為母單元。按照高階插值多項式來構造形狀函式,形成局部坐標系的單元位移函式然後通過坐標變換,將簡單幾何形狀的母單元在總體坐標系中映射成實際格線劃分的曲邊或曲面單元。
實際單元的特性分析(位移、應變、應力等)就可藉助基本單元(母單元)來進行,再將分析結果變換(映射)到實際單元去。由於基本單元形狀規則,因此位移模式容易選取,計算也大為簡單。
等參數單元在構造形函式時首先定義一個規則的母體單元(參考單元/ 標準單元),在母體單元上構造形函式,再通過等參數變換將實際單元與母體單元聯繫起來。
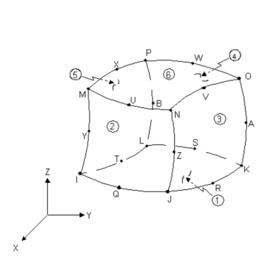
變換涉及兩個方面:幾何圖形的變換(坐標變換) 和位移場函式的變換(母單元的位移模式)分別如圖1、圖2所示。
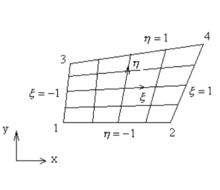 圖1.幾何圖形的變換
圖1.幾何圖形的變換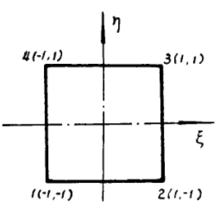 圖2.位移場函式的變換
圖2.位移場函式的變換取四個角點為結點,在單元內的排序為1、2、3、4。仿照矩形單元,可定義出四個形函式:
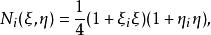 等參數單元
等參數單元其中i=1,2,3,4。
單元的特性分析
採用類似四結點矩形單元的特性分析,可以建立單元應變矩陣、應力矩陣、剛度矩陣、結點力等效的計算公式。
單元應變矩陣
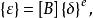 等參數單元
等參數單元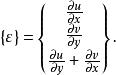 等參數單元
等參數單元其中,
應力矩陣
應力矩陣表達式為:[S]=[D][B].
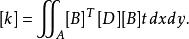 等參數單元
等參數單元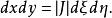 等參數單元
等參數單元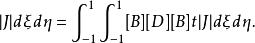 等參數單元
等參數單元單元剛度矩陣是一個8×8的矩陣 ,仍為由於[B]是用局部坐標系ξ、η給出,因此故:
一般而言,等參單元的剛度積分很難有解析式,必須進行數值積分,普遍採用高斯數值積分法。
結點力等效
將作用在單元上的外載荷同樣表示為局部坐標的函式,就可以在局部坐標下完成單元的載荷移置。
體力移置的公式為:
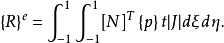 等參數單元
等參數單元單元剛度矩陣
單元剛度矩陣表達式如下所示:
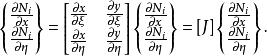 等參數單元
等參數單元稱為雅可比矩陣,由坐標變換式確定,當逆陣存在時,則形函式對x ,y 的導數可求,即應變陣可求。一般而言,等參單元的剛度積分很難有解析式,必須進行數值積分,普遍採用高斯數值積分法。
等參數單元說明
等參單元的幾點說明:
1.等參單元為協調元,滿足有限元解收斂的充要條件;
2.等參單元存在的充要條件是:∣J∣≠0;
3.要求總體坐標系下的單元為凸,即不能有內角大於或等於或接近180 度情況。其中坐標系下單元為凹的多邊形如圖3所示,坐標系下單元為凸的多邊形如圖4所示:
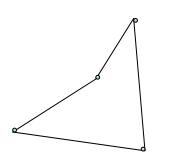 圖3.單元為凹的多邊形
圖3.單元為凹的多邊形 圖4.單元為凸的多邊形
圖4.單元為凸的多邊形單元分析
單元特性分析與結點力計算過程與四結點等參數單元完全相同,具體公式形式也一致。區別僅在於兩種單元有關矩陣的維數不同。四結點單元與八結點單元的區別如表1所示:
| 四結點單元 | 八結點單元 | |
| {δ} | 8×1列陣 | 16×1列陣 |
| [B] | 3×8矩陣, 4個分塊 | 3×16矩陣,8個分塊 |
| [k] | 8×8矩陣 | 16×16矩陣 |
| 面力 | 分到2個結點 | 分到3個結點 |