簡介
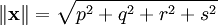
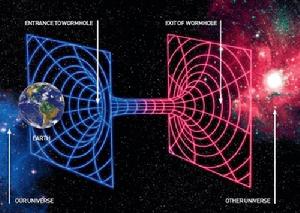
如果我們認為愛因斯坦是錯誤的,c相對任何參考系可能改變,當A速度為c時,光的波長=無限大,光成為一條直線,我們可以理解現在的光量子成為排成一條直線的連續“波”,此時我們的A如果背向一個信息源,這個信息源發出的所有信息我們都無法接收到,我們看到的就是這個信息源在我們運動開始的一瞬間的狀態,而如果我們速度稍微小於光速,則和相對論的預言將會一樣,時間會變慢,波長會增大,如果我們的速度大於光速,則背向信息源運動可以看到這個信息源以前發出的信息,相向信息源發出的光運動,可以提前看到未來,如果說我們處於一大堆信息源圍成的立體幾何體中央,我們必然要在背離一個信息源(時間倒流)的同時選擇靠近一個信息源(看到未來),所以說如果時光倒流可能成立,我們只能像一個背離所有空間方向的方向運動,如同在一條線(左右)上的點向前後移動,比如一個面(前後左右)上的點向上下移動,所以運動的物體必然要向一個處於這個空間中,但是可以背離所有物體的方向運動。
(虛)實時間是矢量,必須有大小和方向。
如果根本不存在時光倒流,我們也可以通過理論得出這樣一個維度存在的結論,通過實驗或許能過測量出這個維度與我們現實世界的三個維度的夾角度數(因為被嚴重捲曲所以不是垂直),暫時沒有人資助這個實驗,但是將來有指望進行證實。
作為空間的第四維度
關於這一點,考克斯特曾寫道:
把時間作為第四維度帶來的好處即使有的話也是微不足道的。實際上,H. G. 威爾在《時間機器》中發展的這種十分吸引人的觀點導致了J. W. 杜恩(《時間實驗》)等作者對相對論的非常錯誤的理解。閔可夫斯基的時空幾何是不符合歐幾里得體系的,所以也就與當前的研究沒有關係。
從數學方面講,普通三維空間集合的四維等價物是歐幾里得四維空間,一個四維歐幾里得賦范向量空間。一個向量的“長度”
x=(p,q,r,s)
以標準基底表示就是
也就是勾股定理向四維空間進行的很自然的類比。這就讓兩個向量之間的夾角很容易定義了。
正交性
在我們熟悉的三維空間裡,有三對主要方向:上下(高度),南北(緯度),東西(經度)。這三對方向兩兩正交,也就是說,它們兩兩成直角。從數學方面講,它們在三條不同的坐標軸x、y、z上。計算機圖形學中講的深度緩衝指的就是這條z軸,在計算機的二維螢幕上代表深度。
純空間性的四維空間另有一對垂直於其他三個主要方向的主要方向。這一對方向處在另一條同時垂直於x、y、z軸的坐標軸上,通常稱作w軸。對這兩個方向的命名,人們的看法不一。一些現行的命名有安娜/卡塔,斯皮希圖/斯帕提圖,維因/維奧,和宇普西龍/德爾塔。這些額外的方向處於(實際上是垂直於)我們所能觀察到的三維世界中的方向之外。