定義
 第一型曲線積分
第一型曲線積分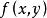 第一型曲線積分
第一型曲線積分 第一型曲線積分
第一型曲線積分 第一型曲線積分
第一型曲線積分 第一型曲線積分
第一型曲線積分 第一型曲線積分
第一型曲線積分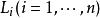 第一型曲線積分
第一型曲線積分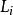 第一型曲線積分
第一型曲線積分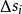 第一型曲線積分
第一型曲線積分 第一型曲線積分
第一型曲線積分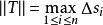 第一型曲線積分
第一型曲線積分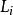 第一型曲線積分
第一型曲線積分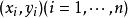 第一型曲線積分
第一型曲線積分設 為平面上可求長度的曲線段, 為定義在 上的函式.對曲線 作分割 ,它把分成 個可求長度的小曲線段 , 的弧長記為 ,分割 的細度為 ,在 上任取一點 , 若存在極限
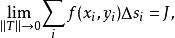 第一型曲線積分
第一型曲線積分 第一型曲線積分
第一型曲線積分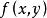 第一型曲線積分
第一型曲線積分 第一型曲線積分
第一型曲線積分且它的值與分割及點的取法無關,則稱此極限 為 在 上的 第一型曲線積分 ,記為
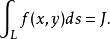 第一型曲線積分
第一型曲線積分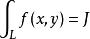 第一型曲線積分
第一型曲線積分或者簡寫成。
 第一型曲線積分
第一型曲線積分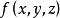 第一型曲線積分
第一型曲線積分 第一型曲線積分
第一型曲線積分 第一型曲線積分
第一型曲線積分 第一型曲線積分
第一型曲線積分 第一型曲線積分
第一型曲線積分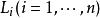 第一型曲線積分
第一型曲線積分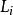 第一型曲線積分
第一型曲線積分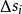 第一型曲線積分
第一型曲線積分 第一型曲線積分
第一型曲線積分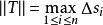 第一型曲線積分
第一型曲線積分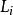 第一型曲線積分
第一型曲線積分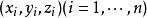 第一型曲線積分
第一型曲線積分設 為空間上可求長度的曲線段, 為定義在 上的函式.對曲線 作分割 ,它把分成 個可求長度的小曲線段 , 的弧長記為 ,分割 的細度為 ,在 上任取一點 , 若存在極限
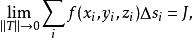 第一型曲線積分
第一型曲線積分 第一型曲線積分
第一型曲線積分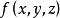 第一型曲線積分
第一型曲線積分 第一型曲線積分
第一型曲線積分且它的值與分割及點的取法無關,則稱此極限 為 在 上的 第一型曲線積分,記為
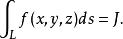 第一型曲線積分
第一型曲線積分對於一般維空間中曲線,可同樣給出定義。
物理意義
 第一型曲線積分
第一型曲線積分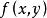 第一型曲線積分
第一型曲線積分 第一型曲線積分
第一型曲線積分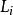 第一型曲線積分
第一型曲線積分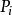 第一型曲線積分
第一型曲線積分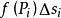 第一型曲線積分
第一型曲線積分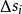 第一型曲線積分
第一型曲線積分當 是平面上某一可求長度的曲線, 是其密度函式,當計算物體的質量問題時便須要第一型曲線積分.首先對 作分割,把分成n個可求長度的小曲線段 (i=1,2,…,n),並在每一個上任取一點 ,由於密度函式為連續函式,故當的弧長都很小時,每一小段的質量可近似地等於 ,其中 為小曲線段的長度.於是在整個上的質量就近似地等於和式
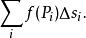 第一型曲線積分
第一型曲線積分 第一型曲線積分
第一型曲線積分當對的分割越來越細密時,上述和式的極限就應是該物體的質量 .
性質
第一型曲線積分具有下述一些重要性質 :
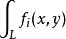 第一型曲線積分
第一型曲線積分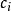 第一型曲線積分
第一型曲線積分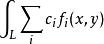 第一型曲線積分
第一型曲線積分1).若存在,為常數,則也存在,且
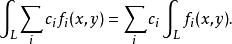 第一型曲線積分
第一型曲線積分 第一型曲線積分
第一型曲線積分 第一型曲線積分
第一型曲線積分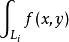 第一型曲線積分
第一型曲線積分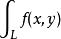 第一型曲線積分
第一型曲線積分2).若曲線段由曲線首尾相接而成,且都存在,則也存在,且
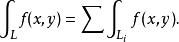 第一型曲線積分
第一型曲線積分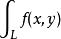 第一型曲線積分
第一型曲線積分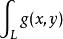 第一型曲線積分
第一型曲線積分 第一型曲線積分
第一型曲線積分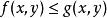 第一型曲線積分
第一型曲線積分3).若與都存在,且在上, 則
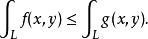 第一型曲線積分
第一型曲線積分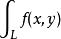 第一型曲線積分
第一型曲線積分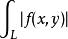 第一型曲線積分
第一型曲線積分4).若存在,則也存在,且
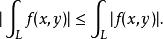 第一型曲線積分
第一型曲線積分第一型曲線積分的計算
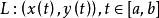 第一型曲線積分
第一型曲線積分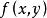 第一型曲線積分
第一型曲線積分 第一型曲線積分
第一型曲線積分設有光滑曲線,函式為定義在上的連續函式,則
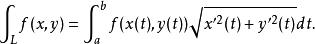 第一型曲線積分
第一型曲線積分套用
下面給出二個常用的套用。
 第一型曲線積分
第一型曲線積分1) 空間曲線的重心坐標為
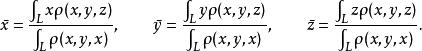 第一型曲線積分
第一型曲線積分 第一型曲線積分
第一型曲線積分2)曲線繞z軸(x, y軸)的轉動慣量 是
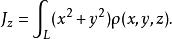 第一型曲線積分
第一型曲線積分