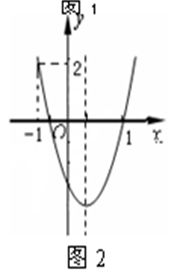
定義
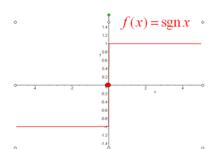符號函式符號函式（signum）可由階躍信號得來。對於符號函式在跳變點可以不予定義，或規定sgn（0）=0。
顯然，可以用階躍信號來表示符號函式：
sgn（x）=2u（t）-1
即 x>0,sgnx=1
x=0,sgnx= 0
x<0,sgnx=-1
性質
用艾佛森括弧定義：
sgn x= − [ x< 0] + [ x> 0]任何實數都可以表示為其絕對值和符號函式的積：
x= (sgn x) | x|若x不為零，可以由上式得出符號函式的另一個定義：
sgn(x)=x/|x|
符號函式是絕對值函式的導數：
d|x|/dx=x/|x| 除了在0，符號函式可微分，其導數為0。透過一般化微分概念，可以說符號函式是狄拉克δ函式的兩倍：
dsgn(x)/dx=2δ（x） 它和單位步階函式的關係：
sgn x= 2 H1 / 2( x) − 1
特性
其定義域為R，值域為{-1,0,1}；
1.其定義域為R，值域為{-1,0,1}；
2.有唯一的跳躍間斷點x=0;
3.單調性：它是不嚴格遞增的非周期函式；
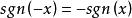符號函式4.奇偶性：由 可知它在定義域R內是奇函式；
5.可導性：它在非原點處都可導，且導數為0；
符號函式6.它在上沒有原函式；
符號函式7.它在任意區間 上都Rieman可積;
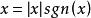符號函式8.。
套用
可用於說明可積函式不一定存在原函式
由於x=0是y=sgn(x)的唯一跳躍間斷點，故在任何以x=0為內點的區間上，sgn(x)不存在原函式。而在任
1.可用於說明可積函式不一定存在原函式
由於x=0是y=sgn(x)的唯一跳躍間斷點，故在任何以x=0為內點的區間上，sgn(x)不存在原函式。而在任
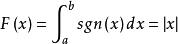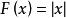符號函式
符號函式何以閉區間[a,b]上Rieman可積，且 ，在x=0處 不可導，F(x)並不是
y=sgn(x)的原函式，說明可積函式不一定存在原函式，有助於弄清楚函式的Rieman可積與存在原函式之間互
不蘊含的關係，還可以作為原函式存在定理中條件f(x)在[a,b]上連續不滿足時，結論不成立的反例，強調條件
不可缺少而引起重視 。
2.用於簡化帶絕對值函式積分的計算
對含有絕對值的函式 ,可先把絕對值去掉化為分段函式求解 ,也可以用一種更為簡單的求解方法 ,就是引入
符號函式來簡化積分的運算。
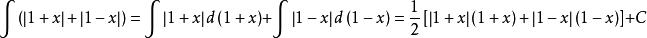符號函式例:
符號函式在積分過程中可視為常數係數，是解題過程簡化。因此對於一些含有絕對值的函式可用此法解決。
