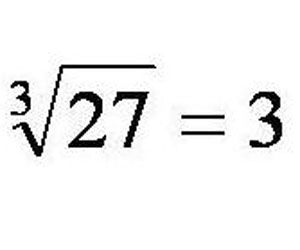概念
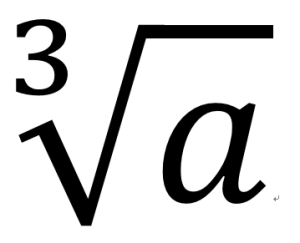 立方根
立方根求一個數a的立方根的運算叫做開立方。
任何數有且只有三個立方根,它們均勻分布在以原點為圓心,算術根為半徑的圓周上,三個立方根對應的點構成正三角形。立方根的性質:⑴任何不是0的數都有3個立方根.⑵0的立方根是0.一般地,如果一個數X的立方等於a,那么這個數X就叫做a的立方根(cuberoot,也叫做三次方根)。也就是說,如果x3=a,那么x叫做a的立方根。,0是0的立方根。
立方和開立方運算,互為逆運算。
在複數範圍內,負數既可以開平方,又可以開立方。在實數範圍內,負數不能開平方,但可以開立方。
與算術根比較
⑴做這兩個數的立方⑵作差
⑶比較被開方數(如三次根號3大於三次根號2)
任何數(正數、負數、或零)的立方根如果存在的話,必定只有3個(重根按重數計算)
區別聯繫
區別
⑴根指數不同:平方根的根指數為2,且可以省略不寫;立方根的根指數為3,且不能省略不寫。⑵結果不同:平方根的結果除0之外,有兩個互為相反的結果;立方根的結果有3個,3個立方根均勻分布在以原點為圓心,算術根為半徑的圓周上,三個立方根對應的點構成正三角形。
聯繫
二者都是與乘方運算互為逆運算函式
C++
求立方根的牛頓法基於如下事實,如果y是x的立方根的一個近似值,那么下式將給出一個更好的近似值:(x/y2+2y)/3請利用這一公式實現一個類似平方根過程的求立方根的過程。
代碼:
#include<iostream>
#include<math>
usingnamespacestd;
floatfun(floatguess,floatx){
if(abs(guess*guess*guess-x)<0.0000001)returnguess;
else
returnfun((x/guess/guess+2*guess)/3,x);
}
intmain()
{
floata,b;
while(cin>>a>>b)
cout<<fun(a,b)<<endl;
return0;
}
JAVA
publicclasstest{publicstaticvoidmain(Stringargv[]){System.out.println(Math.pow(27d,(1/3d)));}}
公式
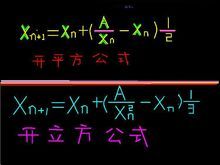 立方根
立方根第一步:
輸入值大於輸出值,負反饋;2-0.25=1.75,取2位數值,即1.7。
第二步:
輸入值小於輸出值,正反饋;取3位數,比前面多取一位數。
第三步:
輸入值大於輸出值,負反饋
第四步:
輸入值小於輸出值,正反饋;
這種方法可以自動調節,第一步與第三步取值偏大,但是計算出來以後輸出值會自動轉小;第二步,第四步輸入值偏小,輸出值自動轉大。當然也可以取1.1,1.2,1.3,。1.8,1.9中的任何一個。
開平方公式
例如,A=5:
5介於2的平方至3的平方;之間。我們取初始值2.1,2.2,2.3,2.4,2.5,2.6,2.7,2.8,2.9都可以,我們最好取中間值2.5。
第一步:2.5+(5/2.5-2.5)1/2=2.2;
即5/2.5=2,2-2.5=-0.5,-0.5×1/2=-0.25,2.5+(-0.25)=2.25,取2位數2.2。
第二步:2.2+(5/2.2-2.2)1/2=2.23;
即5/2.2=2.27272,2.27272-2.2=-0.07272,-0.07272×1/2=-0.03636,2.2+0.03636=2.23。取3位數2.23。
第三步:2.23+(5/2.23-2.23)1/2=2.236。
即5/2.23=2.2421525,,2.2421525-2.23=0.0121525,,0.0121525×1/2=0.00607,,2.23+0.006=2.236.,取4位數。
每一步多取一位數。這個方法又叫反饋開方,即使你輸入一個錯誤的數值,也沒有關係,輸出值會自動調節,接近準確值。