基本概念
穩定性
穩定性，是指系統在擾動消失後，由初始偏差狀態恢復到原平衡狀態的性能。
穩定是控制系統的重要性能，也是系統能夠正常運行的首要條件。
李雅普諾夫穩定性描述
【李雅普諾夫】
對線性系統，若其在初始擾動下，動態過程隨時間推移逐漸衰弱趨近零（原工作點），則稱系統漸進穩定，簡稱穩定；反之，若系統在初始擾動下，動態過程隨時間推移發散，則稱系統不穩定。
誤差（偏差）
如右圖所示的控制系統，
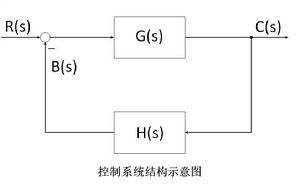穩態誤差係數當輸入信號R(s)和主反饋信號B(s)不等時，比較裝置輸出為：
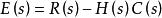穩態誤差係數此時系統在E(s)的信號作用下產生動作，使輸出量趨於希望值。通常稱E(s)為誤差信號，簡稱 誤差（或偏差）。
穩態誤差
控制系統的穩態誤差，是系統控制精度的一種度量，通常稱穩態性能。顯然，當系統穩定時才考慮穩態誤差，所以判斷系統是否穩定是討論進一步求取穩態誤差的必須前提。
由上一目錄，定義系統偏差傳遞函式，
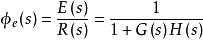穩態誤差係數系統穩態誤差可用拉氏變換終值定理求解：
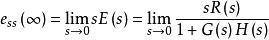穩態誤差係數註解：偏差信號包含瞬態分量和穩態分量，由於已經認定所討論系統必須穩定，瞬態分量最終趨於0，因而用穩態分量代表穩態誤差。
系統類型
一般情況下，分子階次為m，分母階次為n的開環傳遞函式可表示為
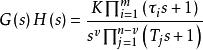穩態誤差係數式中K為開環增益；τ和T為時間常數；v是開環系統在s平面坐標原點上的極點的重數。
以v來對系統進行類型劃分，v為0稱為0型系統，v為1為Ⅰ型系統，以此類推，除複合控制外一般不採用Ⅲ型及以上的系統。
穩態（靜態）誤差係數
靜態誤差係數，是為了方便反映控制系統穩態誤差而設定的係數。結合系統的型別可以快速求出系統的穩態誤差。
相關計算
靜態位置誤差係數
在階躍輸入作用下，即r(t)=R·1(t)，其中R為輸入階躍函式幅值，可以算出穩態誤差為
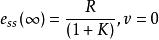穩態誤差係數
穩態誤差係數對於0型單位反饋控制系統，在單位階躍輸入作用下，其穩態誤差是期望輸出1和實際輸出K/(1+K)之間的位置誤差。習慣上定義靜態位置誤差係數Kp表示各型系統在階躍輸入作用下的位置誤差。
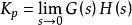穩態誤差係數靜態速度誤差係數
在速度輸入作用下，即r(t)=R·t，其中R為輸入速度函式斜率，可以算出穩態誤差為
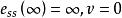穩態誤差係數
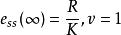穩態誤差係數
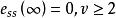穩態誤差係數定義靜態速度誤差係數Kv
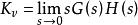穩態誤差係數靜態加速度誤差係數
在加速度輸入作用下，即r(t)=0.5R·t^2，其中R為輸入加速度函式速度變化率，可以算出穩態誤差為
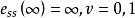穩態誤差係數
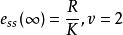穩態誤差係數
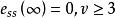穩態誤差係數定義靜態加速度誤差係數Ka
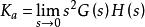穩態誤差係數作用及總結
作用和意義
穩態（靜態）誤差係數定量描述了系統跟蹤不同形式輸入信號的能力。當系統輸入信號形式、輸出量的希望值及容許的穩態位置誤差確定後，可以方便的根據靜態誤差係數去選擇系統的型別和開環增益。但是靜態誤差係數僅對單位反饋控制系統有著明確的物理意義。
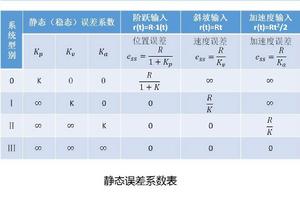
總結表格
可以將三種穩態誤差係數總結表格如下
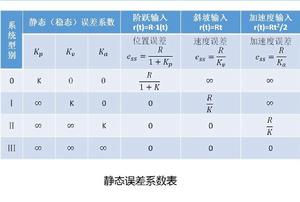穩態誤差係數