問題來源
問題來自於一場“3分鐘相親”活動,參加活動的有n位男士和n位女士。要求每位男士都要和所有的女士進行短暫的單獨交流,並為她們打分,然後按照喜歡程度,對每一位女士進行排序;同樣的,每位女士也要對所有男士進行打分和排序。
對於典型“穩定婚姻問題”,藉助矩陣(二維數組)給出了一種簡明的實現方法。在本算法中,所採用的存儲結構和實現方法靈活巧妙,通俗易懂,方便實現;而且用於存儲所要處理數據的記憶體空間相對於其它一些算法節省了一半,空間複雜度為O(1);由於存儲結構的巧妙性,算法的時間複雜度在最好的情況下為線性時間N,在最壞的情況下為O(N2)。
這個是數學界切切實實研究過的問題。對於以前沒有接觸過這個問題的人,這個理論最出人意外的結論是:傳統的求愛,結婚過程是male-optimal的,也就是說,男性能夠得到儘可能好的心上人,女性卻不然。這就是所謂的穩定匹配問題(StableMarriageProblem,也叫穩定婚姻問題)。
定理
 穩定婚姻問題
穩定婚姻問題穩定婚姻問題。它有很多種可能的解法。為了讓大家相信數學家不是真得如此無聊,我要指出它確確實實是一個地道的組合數學問題,有其特定的數學價值。當然啦,它也有很多別的背景和套用,比如用來在若干個公司和應聘者之間進行招聘中介……但是數學家們怎么會放過如此八卦的一個名字呢?於是它就這樣流傳下來了。
有很多組合數學問題都可以如此這般的翻譯為生活中的問題。比如著名的Hall定理:給定n個有限集合(其間可以有交集),如果其中任意m個集合的並集的元素個數都不小於m,那么一定存在n個不同的元素,使得它們正好依次存在於這n個集合之中。我相信沒有人明白以上這是在說什麼。可是它有一個很好的解釋:把那n個集合想像成n個男生各自心儀的女孩子們(一般來說都不止一個),中間的那個條件是說,如果對於其中任意一部分男生,他們喜歡的女孩子的總數都不少於這組男生的人數(這個條件是必要的,否則就打起來了),那么總的說來一定存在一種辦法給每個男生都分配一個女生恰好是他喜歡的。
活動方式
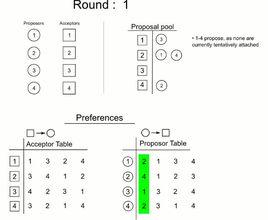
1962年,美國數學家David Gale和Lloyd Shapley發明了一種尋找穩定婚姻的策略,人們稱之為延遲認可算法(Gale-Shapley算法)。
先對所有男士進行落選標記,稱其為自由男。當存在自由男時,進行以下操作:
①每一位自由男在所有尚未拒絕她的女士中選擇一位被他排名最優先的女士;
②每一位女士將正在追求她的自由男與其當前男友進行比較,選擇其中排名優先的男士作為其男友,即若自由男優於當前男友,則拋棄前男友;否則保留其男友,拒絕自由男。
③若某男士被其女友拋棄,重新變成自由男。
在算法執行期間,自由男們主動出擊,依次對最喜歡和次喜歡的女人求愛,一旦被接受,即失去自由身,進入訂婚狀態;而女人們則採取“守株待兔”和“喜新厭舊”策略,對前來求愛的男士進行選擇:若該男子比未婚夫強,則悔婚,選擇新的未婚夫;否則拒絕該男子的求婚。被女友拋棄的男人重獲自由身,重新擁有了追求女人的權利——當然,新的追求對象比不過前女友。
這樣,在算法執行期間,每個人都有可能訂婚多次——也有可能一開始就找到了自己的最愛,從一而終——每訂一次婚,女人們的選擇就會更有利,而男人們的品味則越來越差。只要男女生的數量相等,則經過多輪求婚,訂婚,悔婚和再訂婚之後,每位男女最終都會找到合適的伴侶——雖然不一定是自己的最愛(男人沒能追到自己的最愛,或女人沒有等到自己的最愛來追求),但絕對不會出現“雖然彼此相愛,卻不能在一起”的悲劇,所有人都會組成穩定的婚姻。
求婚過程
第一天上午,所有的男人都向自己最愛的女人求婚,下午,每個女人看看自己有沒有收到,收到了多少人的求婚,如果只收到一個男人的求婚,那么就和他訂婚。如果收到多於一個男人的求婚,那么就和其中她最愛的那個男人訂婚,同時把其他男人都鋸掉。如果一個求婚都沒有,不要著急,最後總會有的。晚上,檢查一遍,如果所有女人都訂婚了,,萬事大吉,明天舉行集體婚禮,但如果還有女人沒有訂婚,那么事情還沒有完,第二天還得重複,第二天上午,所有還沒訂婚的男人向自己次愛的女人求婚(因為昨天已經被他們的最愛鋸了)。下午,每個女人再看一遍自己收到訂婚的情況,如果她已經訂婚了,但是又有一個她更愛的男人來向她求婚,那就把原來那個鋸掉,再和這個更愛的男人訂婚;如果還沒訂婚,那就和第一天的下午的處理一樣。晚上再檢查一遍,如果還是有人沒有訂婚,那第三天再重複,第三天上午,所有沒有訂婚的男人,包括第一天訂了第二天又被踹出來的,再向還沒有鋸過他的女人中他最愛的那個求婚如此周而復始,直到最後大家都訂了婚,便一起結婚。
這么個過程數學上可以證明:
第一,這個過程會中止,也就是說,總有大家都訂了婚的一天,不可能無限循環。
第二,中止後所有的婚姻是穩定婚姻。所謂不穩婚姻是說,比如說有兩對夫婦M1,F1和M2,F2,M1的老婆是F1,但他更愛F2;而F2的老公雖說是M2.但她更愛M1,這樣的婚姻就是不穩婚姻,M1和F2理應結合,他們現在各自的婚姻都是錯誤.我們能證明的是,通過上面那個求婚過程,所有的婚姻都是穩定的,沒有人犯錯誤。
第三,比較引人注目的是,這個過程是male-optimal的,男性能夠獲得儘可能好的伴侶,比如說最後有二十個女人拒絕了他,他仍然能夠得到剩下的八十個女人中他最愛的那一個。
第四,更有甚者,這個過程是female-pessimal的,女人總是在可能的情況下被最不喜歡的人追上。這一點沒有那么直觀的理解,勉強要解釋的話,可以這么看:雖說女人每換一次訂婚對象,都往上升一層,但起點可能很低,雖說在一步步接近她最愛的目標,但最後往往達不到。比如說還差三十名就達到她最愛的人了,但這時GameOver,所有的人都已訂了婚,這樣她也只能死了心了。還有三十個她更愛的人還沒向她求過婚,可是她也無可奈何了,但她仍然能夠得到剩下的七十個男人中她最愛的那一個。
算法
用C++來實現Gale-Shapley算法,採用男士主動求愛,女士接受求愛的方式。
假設男女生人數均為MAX,對每位男士和女士均進行編號,用自然數0,1,2,。。。,MAX-1表示其序號(依照C++的習慣,序號從0開始)。
用二維數組liMan[MAX][MAX]來存儲男士所喜歡的女士序號的排列表;同理,用二維數組libLady[MAX][MAX+1]來存儲女士所喜歡的男士序號的排列表,例如v號女最喜歡i號男,則libLady[v][0]=i;若t號男比i號男更招v號女喜歡,則在數組libLady[v][]中,元素值t的下標小於元素值i的下標。
為了簡化算法,增加一個“不存在”的男士(序號為MAX),作為女士最初的選擇。在給二維數組libLady[MAX][MAX+1]賦初值時,對於任意一個女士v,總有libLady[v][MAX]=MAX。
為所有的男士(包括那個“不存在”的)建立一個數組man[MAX+1],用來存儲他們追求女士的次數,i號男目前追求的女士序號為libMan [man]。
例如,man =0表示i號男尚未追求過女士,其所追求的女士序號為libMan[0];man=2表示i號男已經追求過兩位女士,他下次追求的女士序號為libMan[2](即在喜好表中排名第3位的女士)。
很明顯,man[MAX+1]的每個元素初始值均為0,表示剛開始時,每位男士都去追求自己最喜歡的女士,man 值越大,男士對所選擇的女士越不滿意。
為所有的女士建立一個數組lady[MAX],用來存儲她所選擇的男士序號,數組的所有元素初始值均為MAX,表示女士的當前男友為一個“不存在”的男士,他的分值比任何男士都低,以保證當有一個真正的男人追求該女士時,她會毫不猶豫的拋棄MAX,而選擇該男子。
遍歷數組man[MAX+1],依次讓每個男士去追求自己心儀的女士(當然不需要處理元素man[MAX]——那個“不存在”的男人)。例如現在正逢i號男追求v號女,若i號男不如v號女當前男友,則遭拒絕,i號男繼續追求其“次喜歡女”;反之,若i號男比v號女當前男友優秀,則v拋棄前男友,選擇i號男為新男友,而其前男友(設為t號男)重獲自由身,可以去追求自己的“次喜歡女”了。
這裡有一個地方要注意:因為是通過執行(i++)來遍歷數組的,所以如果當t<i時,必須要讓i折回到t位置(使i=t),否則會漏掉t。
當i==MAX時,表示所有男士都找到了自己的另一半,算法結束,輸出結果。
C++代碼如下:
#include<iostream>
usingnamespacestd;
constintMAX=4;
boolChangeFriend(constintlibLady[][MAX+1],intv,intoldF,intnewF);//判斷是否需要換男友
intmain()
intlibMan[MAX][MAX]={{2,1,3,0},{0,2,3,1},{2,3,1,0},{1,3,2,0}};//存儲男士所喜歡的女士序號的排列表
intlibLady[MAX][MAX+1]={{0,3,1,2,MAX},{1,3,2,3,MAX},{0,2,3,1,MAX},{1,0,3,2,MAX}};//存儲女士所喜歡的男士序號的排列表
intman[MAX+1]={0};
intlady[MAX]={MAX,MAX,MAX,MAX};
inti=0;
while(i<MAX)
intv=libMan [man];//i號男喜歡v號女
if(i==lady[v])//i號男就是v號女當前男友,跳過,處理下一個男士
i++;
elseif(ChangeFriend(libLady,v,lady[v],i))//若i號男比v號女當前男友優秀,則v拋棄前男友,重新選擇i
intt=lady[v];//存儲前男友序號
man[lady[v]]++;//拋棄前男友,即前男友選擇其“次喜歡女”
lady[v]=i;//選擇i號男為新男友
if(t>i)//前男友序號t在新男友i之後,則今後順序前行可以處理t
i++;//處理下一個男士
else//前男友序號t在新男友i之前,返回t,否則會漏掉t
i=t;
else//繼續處理i號男的“次喜歡女”
man ++;
for(inti=0;i<MAX;i++)//輸出每位男士追求女士的次數
cout<<man +1<<",";
cout<<endl;
for(inti=0;i<MAX;i++)//輸出每位男士的妻子的序號
cout<<libMan [man]<<",";
cout<<endl;
for(inti=0;i<MAX;i++)//輸出每位女士的丈夫的序號
cout<<lady <<",";
cout<<endl;
system("pause");
return0;
boolChangeFriend(constintlibLady[][MAX+1],intv,intoldF,intnewF)//判斷是否需要換男友
for(inti=0;i<=MAX;i++)
if(libLady[v] ==oldF)
oldF=i;
break;
for(inti=0;i<=MAX;i++)
if(libLady[v] ==newF)
newF=i;
break;
return(oldF>newF);
在上述實現中,設計了一個子函式boolChangeFriend(constintlibLady[][MAX+1],intv,intoldF,intnewF),用來判斷女士v是否需要換男友,若男子序號newF在數組libLady[v] 的位置比oldF靠前,則說明女士v更喜歡newF,需要換男友,否則不換。通過比較它們的下標,可以得出結論。
這個子函式的引入可以讓程式完成工作,但也帶來一些效率上問題,每次調用函式都要分別遍歷數組libLady[v][]兩次,去尋找oldF和newF的下標,這樣在MAX值很大的時候,時間消耗是相當大的。
另外,由於我們是通過執行(i++)來遍歷數組,每次遇到(t<i)時,都要令i折回到t,然後再執行(i++),進行了很多重複的比較,浪費了寶貴的時間。
首先解決關於子函式的問題。之所以引入子函式,是因為數組libLady[v][]存儲的是女士v所喜歡的男士序號的排列表,而不是男士的分值表。如果我們創建一個二維數組libladyValue[MAX][MAX+1],用來存儲女士v所喜歡的男士的分值,即數組元素libladyValue[v] 表示女士v給i號男打的分數,分數越高,則表示越招人喜歡。這樣我們在判斷女士v是否需要換男友時,就無需遍歷數組,只要直接比較libladyValue[v]和libladyValue[v][t]的值就好了。
其次解決重複比較的問題。我們可以創建一個棧,把所有自由男的序號存儲到棧中,每當有男子訂婚,則將其序號出棧;每當有男子被拋棄,則將其序號入棧。這樣就可以確保不會出現重複比較了。