定義
為了給定n階積和式的定義,我們來定義一下幾個名稱:
線性函式
設f是F^n上的一個k元函式。如果對每一個i,1≤i≤k,均有
f( ξ1,..., ξ(i-1),λ η+μ ζ, ξ(i+1),..., ξk)=λf( ξ1,..., ξ(i-1), η, ξ(i+1),..., ξk)+μf( ξ1,..., ξ(i-1), ζ, ξ(i+1),..., ξk)
其中λ,μ∈F, η, ζ∈F^n,則f稱為 k重線性函式。
規範
設f( ξ1, ξ2,..., ξn)是F^n上的n元函式,且設 εi為第i個分量為1,其他分量為0的向量,i=1,2,...,n。如果f( ε1, ε2,..., εn)=1,則稱f( ξ1, ξ2,..., ξn)是規範的。
對稱
設f( ξ1, ξ2,..., ξn)是F^n上的n元函式,如果對於任意整數i,j,1≤i,j≤n,均有
f( ξ1,..., ξi,..., ξj,..., ξk)=f( ξ1,..., ξj,..., ξi,..., ξk)
則稱f( ξ1, ξ2,..., ξn)是對稱的。
於是我們得到了n階積和式的定義:
積和式定義
給定一個數域F,則稱數域F 上的 規範對稱n重線性函式叫做n階積和式(permanent)。
這和n階行列式對比:
給定一個數域F,則稱數域F 上的 規範反對稱n重線性函式叫做n階行列式(determinant)。
性質
對於一個方陣 A, A=(a),n階積和式記為per A或者perm A
不難證明,
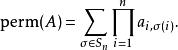 積和式
積和式特殊情況,當n=2時,per A=aa+aa,與行列式只差個符號。因此,積和式有些性質可以類比於行列式。
組合上的解釋
積和式的定義可以從如下兩方面理解,即計算二分圖上完美匹配的個數,以及計算一個圖上的圈覆蓋的權重。
二分圖
二分圖上的完美匹配是算法理論和計算複雜性理論中的重要問題。對於一個n×n的二分圖 G=( L, R, E),其中 L={1, 2,..., n}是左邊結點的集合, R={1', 2', ..., n'}是右邊結點的集合, E為邊的集合, G的一個完美匹配是{1, 2, ..., n}到{1', 2', ..., n'}的一個雙射f,使得(1, f(1)), (2, f(2)), ..., (n, f(n))都在 E中出現。
對 G,我們可以建立如下n×n的0-1矩陣 Ag=(aij),i,j∈{1,2,...,n},其中aij=1若且唯若(i,j')屬於 E。不難驗證,per Ag的值即是 G中完美匹配的個數。這樣,我們將積和式的值與二分圖完美匹配的個數建立了聯繫。
圖的圈覆蓋
對於一個圖 G=( V, E),V={1, 2, ..., n}為結點集, E為邊集。一個 G的圈覆蓋是一組 G中的不相交的圈的集合,且這些圈覆蓋所有的點集。由於一個置換可以做環狀分解,可以看出一個置換與一個可能的圈覆蓋是一一對應的。特別的, G的鄰接矩陣的積和式即是 G中圈覆蓋的數目。
計算複雜性
積和式的計算是#P完全的。相對的,行列式可以用高斯消元法等算法在多項式時間內解決。

