內容
定理
如果函式f(x,y)在有界閉區域D上連續,區域D的面積為S,且 m 和 M 分別是f(x)在D上的最小值和最大值,則mS ≤ ∫∫f(x,y)在D上的二重積分 ≤ MS這就是二重積分的估值定理
計算
如果是一元函式f(x)在區間[a,b]上的定積分,只需把上述估值定理公式中的S改成區間長度 b -a
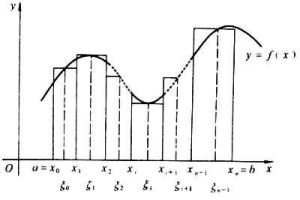
如區間在【n+1,n】單調遞減的函式f(x)的積分
(n+1-n)*f(n+1)<= ∫f(x)dx<=f(n) *(n+1-n)
即任意一個函式在閉區間【a,b】上連續他從閉區間【a,b】的定積分
m(b-a)<=[b,a]∫f(x)<=M(b-a)
其中m為f(x)在閉區間【a,b】上的最小值,M為最大值。
二重積分的性質
性質1 被積函式的常數因子可以提到積分符號的外面去。
性質2 有限個函式代數和的二重積分等於各函式的二重積分的代數和.
性質3 如果把積分區域D分成兩個閉子集和,即D=+,則
性質4 如果在D上f(x,y)
性質5 如果在D上,則
這個性質的幾何意義表示曲頂柱體的積極的數值介於分別以被積函式的最小值和最大值為高,以D為底的兩個平頂柱體體積的數值之間.
性質6 (中值定理)如果函式
這個性質的幾何意義表示在區域D上以曲面f(x,y)為頂的曲頂柱體的體積等於以被積函式在D上的某一函式值為高,D為底的平頂柱體的體積.
性質7 如果積分區域的面積為S,則
性質不證明,給與幾何解釋.
這個性質的幾何意義表示高為1的平頂柱體的體積在數值上正好等於該柱體的底面積.
用不等式組表示積分區域
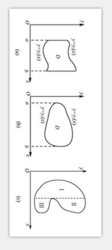
在對二重積分作計算時,我們要將積分區域用一種典型的不等式組來表示.先考慮xOy平面上一種特殊類型的區域,這種區域的特點是:任何平行於x軸或y軸的直線與這一區域的邊界的交點不多於兩個(如圖6-4(a)(b)所示),但是它的邊界曲線可以包含平行於坐標軸的線段(如圖6-4(a)所示).我們常遇到的平面域都可以看作是由若干個這種特殊類型域組合而成的.例如圖6-4(c)所示的區域就可以劃分成三個上述特殊區域.
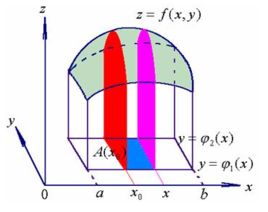
在圖6-1(a)中,設D上點的橫坐標x的變化範圍為[a,b],D的邊界曲線由兩個函式上任何一點x,過點x作一直線平行於y軸,此直線與曲線於是點.由此可見,D上以此x值為橫坐標的一切點的縱坐標y都滿足不等式 。
圖6-4
 6-4
6-4歷史背景
笛卡兒
沒有任何東西比幾何圖形更容易引入腦際,因此用這種方式表達事物是非常有益的.
希爾伯特
算數符號是文字化的圖形,而幾何圖形則是圖像化的公式;沒有一個數學家能缺少這些圖像化的公式.
數學家高斯
高斯(1777~1855)是德國數學家,也是科學家,他和牛頓、阿基米德被譽為有史以來的三大數學家.高斯是近代數學奠基者之一,在歷史上影響之大可以和阿基米德、牛頓、歐拉並列,有“數學王子”之稱.他幼年時就表現出超人的數學天才,十歲時計算從1到100連續100個自然數之和採用的速算法,一直被傳為佳話.1795年他進入哥廷根大學學習,第二年他就發現正十七邊形的尺規作圖法,並給出可用尺規作出正多邊形的條件,解決了歐幾里得以來懸而未決的問題.
高斯的數學研究幾乎遍及所有領域,在數論、代數學、非歐幾何、複變函數和微分幾何等方面都做出了開創性的貢獻.他還把數學套用於天文學、大地測量學和磁學的研究,發明了最小二乘法原理.高斯的數論研究總結在《算數研究》(1801)中,這本書奠定了近代數論的基礎,它不僅是數論方面的劃時代之作,也是數學史上不可多得的經典著作之一.高斯對代數學的重要貢獻是證明了代數基本定理,他的存在性證明開創了數學研究的新途徑.1828年高斯出版了《關於曲面的一般研究》,全面系統的闡述了空間曲面的微分幾何學,並提出內蘊曲面理論.高斯的曲面理論後來由黎曼發展.高斯一生共發表155篇論文,他對待學問十分嚴謹,只是把他自己認為是十分成熟的作品發表出來.其著作還有《地磁概念》和《論與距離平方成反比的引力和斥力的普遍定律》等.
1801年高斯有機會戲劇性地施展他的優勢計算技巧.那年元旦,有一個後來被認為是小行星並被命名為穀神星的天體被發現,當時他好像在向太陽靠近,天文學家雖然有40天的時間可以觀察它,但還不能計算出它的軌道.高斯只作了3次觀測就提出了一種計算軌道參數的方法,而且達到的精確度使得天文學家在1801年末和1802年初能夠毫無困難地再確定穀神星的位置.高斯在這一計算方法中用到了他大約在1794年創造的最小二乘法(一種可從特定計算得到最小的方差和中求出最佳話值的方法),在天文學中這一成就立即得到公認.他在《天體運動理論》中敘述的方法今天仍在使用,只要稍作修改就能適應現代計算機的要求.高斯在小行星“智神星”方面也獲得類似的成功.由於高斯在數學、天文學、大地測量學和物理學中的傑出研究成果,他被選為許多科學院和學術團體的成員.“數學王子”的稱號是對他一生恰如其分的讚頌.
 積分估值定理
積分估值定理