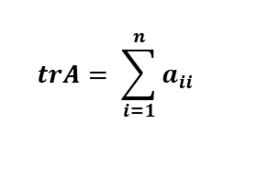矩陣的跡
英文名稱: trace
性質
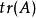 矩陣的跡
矩陣的跡(1)設有N階矩陣A,那么矩陣A的跡(用表示)就等於A的特徵值的總和,也即矩陣A的主對角線元素的總和。
1.跡是所有對角元的和
2.跡是所有特徵值的和
3.某些時候也利用tr(AB)=tr(BA)來求跡
4.tr(mA+nB)=m tr(A)+n tr(B)
(2)奇異值分解(Singular value decomposition )
奇異值分解非常有用,對於矩陣A(p*q),存在U(p*p),V(q*q),B(p*q)(由對角陣與增廣行或列組成),滿足A = U*B*V
U和V中分別是A的奇異向量,而B是A的奇異值。AA'的特徵向量組成U,特徵值組成B'B,A'A的特徵向量組成V,特徵值(與AA'相同)組成BB'。因此,奇異值分解和特徵值問題緊密聯繫。
如果A是復矩陣,B中的奇異值仍然是實數。
SVD提供了一些關於A的信息,例如非零奇異值的數目(B的階數)和A的階數相同,一旦階數確定,那么U的前k列構成了A的列向量空間的正交基。
(3)在數值分析中,由於數值計算誤差,測量誤差,噪聲以及病態矩陣,零奇異值通常顯示為很小的數目。
將一個矩陣分解為比較簡單或者性質比較熟悉的矩陣之組合,方便討論和計算。由於矩陣的特徵值和特徵向量在化矩陣為對角形的問題中占有特殊位置, 因此矩陣的特徵值分解。儘管矩陣的特徵值具有非常好的性質,但是並不是總能正確地表示矩陣的“大小”。矩陣的奇異值和按奇異值分解是矩陣理論和套用中十分重要的內容,已成為多變數反饋控制系統最重要最基本的分析工具之一,奇異值實際上是複數標量絕對值概念的推廣, 表示了反饋控制系統的輸出/輸入增益,能反映控制系統的特性。《魯棒控制.傾斜轉彎飛彈》