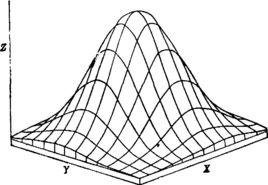
定義
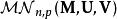矩陣常態分配隨機矩陣X（n×p）的機率密度函式遵循矩陣常態分配 具有以下形式：
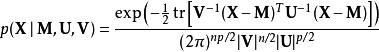矩陣常態分配
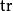矩陣常態分配其中 表示軌跡，M是n×p，U是n×n，V是p×p。
矩陣法線通過以下方式與多元常態分配相關：
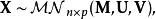矩陣常態分配若且唯若
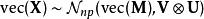矩陣常態分配
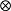矩陣常態分配
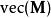矩陣常態分配
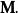矩陣常態分配其中 表示Kronecker積， 表示 的矢量化。
證明
可以使用跡線和Kronecker乘積的若干屬性來顯示上述矩陣法線函式和多元法線密度函式之間的等價，如下所示。我們從矩陣法線PDF的指數的參數開始：
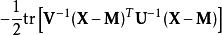矩陣常態分配
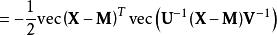矩陣常態分配
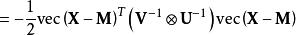矩陣常態分配
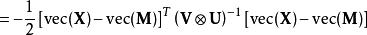矩陣常態分配
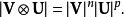矩陣常態分配這是多元法線PDF的指數的參數。使用行列式屬性完成證明：
屬性
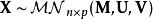矩陣常態分配如果 ，然後我們有以下屬性：
預期值
平均值或預期值為：
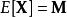矩陣常態分配我們有以下二階預期：
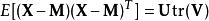矩陣常態分配
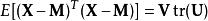矩陣常態分配 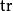矩陣常態分配其中 表示跟蹤。
更一般地，對於適當尺寸的矩陣A，B，C：
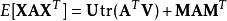矩陣常態分配
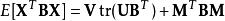矩陣常態分配
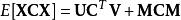矩陣常態分配轉換
轉置變換：
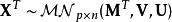矩陣常態分配線性變換：令D（r-by-n），滿秩r≤n且C（p-by-s），滿秩s≤p，則：
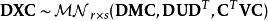矩陣常態分配例子
讓我們構想根據多元常態分配相同分布的n個獨立p維隨機變數的樣本：
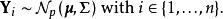矩陣常態分配
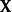矩陣常態分配
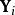矩陣常態分配當定義第i行為的n×p矩陣時，我們得到：
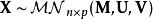矩陣常態分配
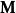矩陣常態分配
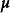矩陣常態分配
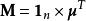矩陣常態分配
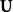矩陣常態分配
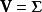矩陣常態分配其中的每一行等於，即，是n×n單位矩陣，即行是獨立的，。
最大似然估計
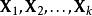矩陣常態分配給定k個矩陣，每個大小為n×p，表示為，我們假設已對其進行了採樣iid從矩陣常態分配，可以通過最大化獲得參數的最大似然估計：
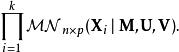矩陣常態分配平均值的解決方案具有封閉形式，即
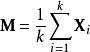矩陣常態分配但協方差參數沒有。但是，這些參數可以通過將其梯度歸零來疊代地最大化：
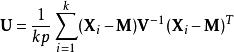矩陣常態分配和
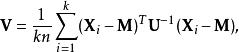矩陣常態分配協方差參數在某種意義上是不可識別的，對於任何比例因子，s> 0，我們有：
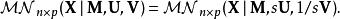矩陣常態分配從分布中繪製值
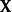矩陣常態分配矩陣常態分配的採樣是多元常態分配的採樣過程的特例。 讓為來自標準常態分配的np個獨立樣本的n×p矩陣，因此
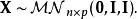矩陣常態分配然後讓
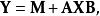矩陣常態分配因此
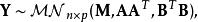矩陣常態分配其中A和B可以通過Cholesky分解或類似的矩陣平方根運算來選擇。
