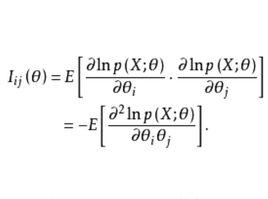基本介紹
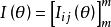 費歇耳信息矩陣
費歇耳信息矩陣一個樣本觀測值所能提供的關於未知多維參數θ=(θ,θ,…θ)的信息量期望值的一種度量——m×m矩陣 ,其中
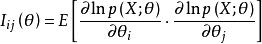 費歇耳信息矩陣
費歇耳信息矩陣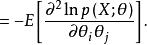 費歇耳信息矩陣
費歇耳信息矩陣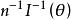 費歇耳信息矩陣
費歇耳信息矩陣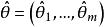 費歇耳信息矩陣
費歇耳信息矩陣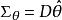 費歇耳信息矩陣
費歇耳信息矩陣 費歇耳信息矩陣
費歇耳信息矩陣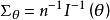 費歇耳信息矩陣
費歇耳信息矩陣式中p(x;θ)為總體X的機率函式。來自總體X的簡單隨機樣本(X,X,…,X)所能提供的關於θ的費歇耳信息量為nI(θ)。這時, 是克拉默-拉奧方差界在多維情況下的類似:設 是θ=(θ,θ,…,θ)的任一無偏估計量, 是 的方差矩陣,則 是非負定矩陣 。
假設(X,Y)有二元常態分配,EX=EY =0,DX=DY =σ ,X和Y的相關係數為ρ,則參數θ=(σ ,ρ)的費歇耳信息矩陣為:
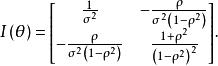 費歇耳信息矩陣
費歇耳信息矩陣相關概念
費歇耳信息量
費歇耳信息量是一次觀測值所能提供的關於未知參數θ的信息量期望值的一種度量,定義為
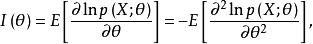 費歇耳信息矩陣
費歇耳信息矩陣其中p(x;θ)是總體的機率函式。
費歇耳信息量I(θ)具有如下性質:
1. 非負性:I(θ)≥0而I(θ)=0若且唯若p(x; θ)不依賴於θ;
2.可加性:n次獨立重複觀測值、即來自總體的簡 單隨機樣本(X,X,…,X)所能提供的關於θ的信息量期望值為nI(θ)。
對於正態總體X~N(μ,σ);I(μ)=1/σ ,I(σ )=1/(2σ );對於參數為λ的泊松總體,I(λ)=1/λ。
克拉默-拉奧方差界
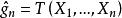 費歇耳信息矩陣
費歇耳信息矩陣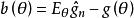 費歇耳信息矩陣
費歇耳信息矩陣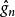 費歇耳信息矩陣
費歇耳信息矩陣克拉默-拉奧方差界是未知參數之一切可能估計量的方差的公共下界。 設總體X的機率函式p(x;θ)依賴於未知參數θ;g=g(θ)是參數θ的函式, 是g的估計量,其中X,…,X是來自X的簡單隨機樣本; 是估計量 的偏倚,則
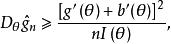 費歇耳信息矩陣
費歇耳信息矩陣 費歇耳信息矩陣
費歇耳信息矩陣其中I(θ)是θ的費歇耳信息量。此不等式稱做“克拉默-拉奧(Cramer-Rao)不等式”,其右側稱做“克拉默-拉奧方差界”。 若 是θ的無偏估計, 則有
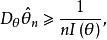 費歇耳信息矩陣
費歇耳信息矩陣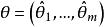 費歇耳信息矩陣
費歇耳信息矩陣對於 是多維參數的情形, 有類似的結果。