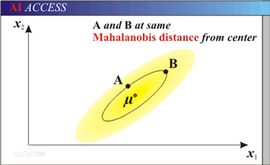
概念
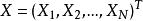 協方差矩陣
協方差矩陣設 為n維隨機變數,稱矩陣
 協方差矩陣
協方差矩陣 協方差矩陣
協方差矩陣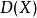 協方差矩陣
協方差矩陣為n維隨機變數 的協方差矩陣(covariance matrix),也記為 ,其中
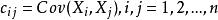 協方差矩陣
協方差矩陣 協方差矩陣
協方差矩陣 協方差矩陣
協方差矩陣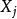 協方差矩陣
協方差矩陣為 的分量 和 的協方差(設它們都存在)。
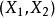 協方差矩陣
協方差矩陣例如,二維隨機變數 的協方差矩陣為
 協方差矩陣
協方差矩陣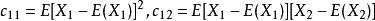 協方差矩陣
協方差矩陣其中
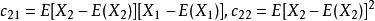 協方差矩陣
協方差矩陣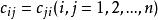 協方差矩陣
協方差矩陣由於 ,所以協方差矩陣為對稱非負定矩陣。
性質
協方差矩陣具有如下性質:
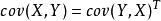 協方差矩陣
協方差矩陣(1) .
 協方差矩陣
協方差矩陣(2) ,其中A是矩陣,b是向量。
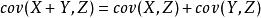 協方差矩陣
協方差矩陣(3) 。
套用
 協方差矩陣
協方差矩陣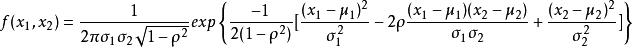 協方差矩陣
協方差矩陣協方差矩陣可用來表示多維隨機變數的機率密度,從而可通過協方差矩陣達到對多維隨機變數的研究。以二維隨機變數 為例,由於
引入矩陣
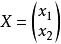 協方差矩陣
協方差矩陣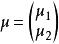 協方差矩陣
協方差矩陣,
 協方差矩陣
協方差矩陣及 的協方差矩陣
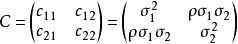 協方差矩陣
協方差矩陣由此可得
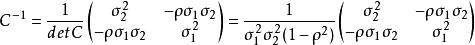 協方差矩陣
協方差矩陣由於
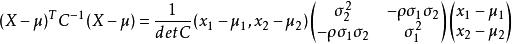 協方差矩陣
協方差矩陣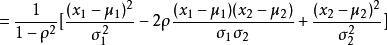 協方差矩陣
協方差矩陣 協方差矩陣
協方差矩陣於是的機率密度
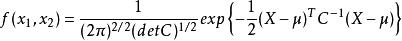 協方差矩陣
協方差矩陣此式可以推廣到n維常態分配的情形。