矛盾方程組及其求解
由線性代數理論知，求解線性方程組時，若方程式的個數多於未知數的個數，則方程組往往無解，此類方程組稱為 矛盾方程組(或 超定方程組)。最小二乘法是用來解矛盾方程組的一個常用方法 。
設有矛盾方程組
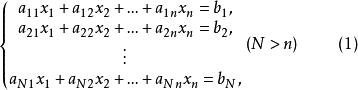矛盾方程組或寫為
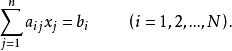矛盾方程組通常找不到能同時滿足方程組(1)的解，因此我們轉而去尋求在某種意義下的近似解，這種近似解不是指對精確解的近似(因為精確解並不存在)，而是指尋求各未知數的一組值，使方程組(1)中各式能近似相等。這就是用 最小二乘法 解矛盾方程組的基本思想。把近似解代入方程組(1)後，只能使各方程式的兩端近似相等，不妨記各個方程式兩端之差為
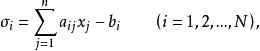矛盾方程組並稱該差為 偏差。按最小二乘原理，採用使偏差的平方和
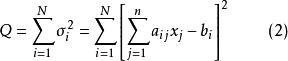矛盾方程組達到最小值來作為衡量一個近似解的近似程度的標誌 。
相關概念及定理
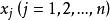矛盾方程組定義1 如果 的取值使偏差平方和即式(2)達到最小，則稱這組值是 矛盾方程組(1)的最優近似解 。
預備知識：
(1) 矩陣的秩。設矩陣 A有一個n階子式D，其不等於0，而n+1階子式皆為0，那么n稱為 A的秩。
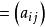矛盾方程組(2) 對稱矩陣。如果n階方陣 A ，滿足 A=A，即
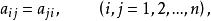矛盾方程組則稱 A為對稱矩陣。
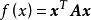矛盾方程組
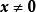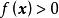矛盾方程組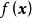
矛盾方程組
矛盾方程組(3) 正定矩陣。設有實二次型 ，如果對於任何 ，都有 ，則稱 為 正定二次型，對稱矩陣 A是正定的。
如果 A為正定矩陣，則 A的特徵值皆為正的。且 A的各階主子式皆為正。
矛盾方程組 矛盾方程組 矛盾方程組 矛盾方程組(4) 矩陣的特徵值。設 A為n階方陣，如果存在常數及非零的n維列向量 X，使 AX= X成立，則稱是方陣 A的特徵值。非零向量 X稱為方陣 A的屬於特徵值的特徵向量。
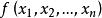矛盾方程組
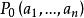矛盾方程組定理1 設n元實函式 在點 的某個鄰域內連續，且有一階及二階連續的偏導數，如果
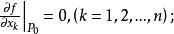矛盾方程組（1）
（2）矩陣
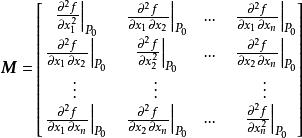矛盾方程組
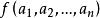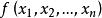矛盾方程組 矛盾方程組是正定矩陣，則 是n元實函式 的極值。
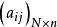矛盾方程組定理2 設非齊次線性方程組 Ax=b的係數矩陣 A= ，若rank A=n，則
(1) 矩陣 AA是對稱正定矩陣；
(2) n階線性方程組 A Ax= Ab有唯一的解。
下面我們討論此二次函式是否存在最小值，若存在，如何求最小值?由高等數學可知，有以下定理。
定理3 設矛盾方程組(1)的係數矩陣 A的秩為n，則二次函式
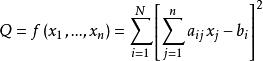矛盾方程組一定存在最小值。
通常稱線性方程組 A Ax= Ab為 正則方程組。只要矛盾方程組(1)的係數矩陣 A的秩rank A=n，則由定理3可以得出：
(1)矛盾方程組(1)的最小二乘解存在；
(2)正則方程組 A Ax= Ab有唯一解，此解就是矛盾方程組(1)的最小二乘解。
用最小二乘法求解矛盾方程組 Ax= b的步驟歸納如下：
(1)計算 AA和 Ab，得正則方程組 A Ax= Ab；
(2)求解正則方程組，得出矛盾方程組的最優近似解 。
