超定方程組
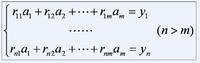超定方程組
超定方程組
超定方程組的解
超定方程一般是不存在解的矛盾方程。
例如，如果給定的三點不在一條直線上， 我們將無法得到這樣一條直線，使得這條直線同時經過給定這三個點。 也就是說給定的條件（限制）過於嚴格， 導致解不存在。在實驗數據處理和曲線擬合問題中，求解超定方程組非常普遍。比較常用的方法是最小二乘法。形象的說，就是在無法完全滿足給定的這些條件的情況下，求一個最接近的解。
曲線擬合是最小二乘法要解決的問題，實際上就是求以上超定方程組的最小二乘解的問題。
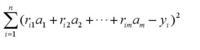超定方程組如果有向量a使得下式的值達到最小，則稱a為上述 超定方程的最小二乘解。
最小二乘解的存在性和唯一性
方程組有精確解，則稱為是相容的，其充要條件是rank(R)=rank(R,y)。設rank(R)=r>0，則總存在分解R=FG，即滿秩分解。
定理1
方程組必存在最小二乘解，且a是方程組的最小二乘解的充要條件是a是RT·R·a=RT·y的解。
定理2
若rank(R)=r<m，則方程組有無窮多個最小二乘解，其中2-範數最小的解稱為方程組的極小最小二乘解，且該解是唯一的，為a'=GT(GGT)-1(FTF)-1FTy
定理3
若rank(R)=m<=n，以上超定方程組存在唯一最小二乘解，解為a=(RT·R)-1·RT·y
