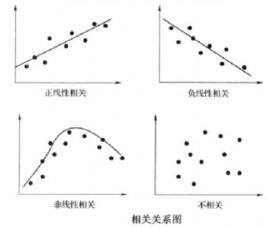
定義
相關圖(Scattor Diagram)又叫 散布圖,指把兩個變數之間的相關關係,用直角坐標系表示的圖表。在工業生產和科學研究中,經常遇到兩個之間的關係問題: 一種是兩個量之間是完全確定的 函式關係;另一 種是兩個量之間是不完全確定的 對應關係。對於這種既相關又不完全確定的關係,就稱為 相關關係。人們套用畫相關圖,求出相關係數的方法來確定兩個量之間的相關關係,就稱為 相關分析。 而當確定了相關關係之後,再用 統計檢驗與估計的方法對相關係數進行判斷並求出回歸方程的作法,稱為 回歸分析 。
相關圖的形式
相關圖的形式多種多樣,可歸納為以下幾種:
(1) 正強相關(x增大,y迅速 增大),見圖1;
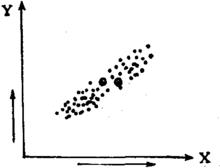 圖1
圖1(2)正弱相關(x增大,y緩慢增大), 見圖2;
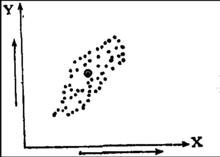 圖2
圖2(3)負強相關(x增大,y迅速下降) ,見圖3;
 圖3
圖3(4) 負弱相關(x增大,y緩慢下降),見圖4;
 圖4
圖4(5) 曲線相關(不成直線關係),見圖5;
 圖5
圖5(6) 無相關(y不隨x增減呈線性關係),見圖6 。
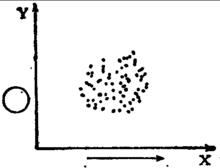 圖6
圖6函式關係與相關關係
客觀現象之間總是相互聯繫和相互依存的,現象之間的數量依存關係有兩種不同的類型:一種是 函式關係,另一種是 相關關係。
當一個或幾個變數取一定的值時,另一個變數有確定值與之相對應,我們稱這種確定性的關係為 函式關係。例如,某種商品的銷售收人Y 與該商品的銷售量X 以及該商品的價格P之間的關係可用Y=PX表示。
當一個或幾個相互聯繫的變數取一定數值時,與之相對應的另一變數的值雖然不確定,但它仍按某種規律在一定範圍內變化,變數間的這種具有不確定性的相互關係,稱為 相關關係。例如,勞動生產率與工資水平的關係、投資額與國民收人的關係、居民收人與消費支出的關係等都屬於相關關係。商品需求量與該商品的價格、消費者的收入水平、消費者的偏好等的關係也屬於相關關係 。
相關關係的種類
按相關程度劃分
按客觀現象間相關關係的密切程度不同可分為 完全相關、 不完全相關和 不相 關三種類型。
當一種現象的數量變化完全由另一種現象的數量變化所確定時,稱這兩種現象間的關係為 完全相關。因此也可以說函式關係是相關關係的一個特例。當兩個現象彼此互不影響,其數量變化各自獨立時,稱為 不相關。例如,經濟發展水平與精神病患者的人數是不相關的。當兩個現象之間的關係介於完全相關和不相關之間時,稱其為 不完全相關。一般說的相關現象都是指這種不完全相關關係。
按變數多少劃分
按所研究的變數多少,相關關係可分為 單相關、 復相關和 偏相關。
我們把兩個變數間的相關,即一個變數對另一個變數的相關關係,稱為 單相 關,單相關關係只有一個自變數。當所研究的是一個變數對兩個或兩個以上其他變數的相關關係時,稱為 復相 關。復相關關係有多個自變數。例如,某種商品的需求量與該商品價格以及消費者收人水平之間的相關關係便屬於復相關。在某一現象與多種現象相關的場合,當假定其他變數不變時,其中兩個變數的相關關係稱為 偏相關。如在上例中,若假定在消費者收入水平不變的條件下,商品需求量與其價格水平的關係就是偏相關關係。
按相關方向劃分
按相關關係的方向可分為 正相關和 負相關。
當兩個變數的變化同方向時,這種同方向變動的關係稱為 正相關。例如,居民的消費支出隨著居民收入水平的提高而提高。當兩個變數的變化反方向時,這種反方向變動的關係稱為 負相關。例如,一定範圍內,商品生產的規模越大,單位產品成本會越低。
按相關形式劃分
相關關係按相關的形式不同可分為 線性相關和 非線性相關。當兩種相關現象之間的關係大致呈現為直線關係時,稱之為 線性相關或直線相關。例如,人均消費水平與人均收入水平之間通常呈線性關係。如果兩種相關現象之間並不表現為直線的關係,而是近似於某種曲線方程的關係,則這種相關關係稱為 非線性相關或曲線相關。例如,某種產品的平均成本與產品總產量之間的關係就屬於非線性相關關係 。