基本概況
 相遇問題圖示
相遇問題圖示兩個物體從兩地出發,相向而行,經過一段時間,必然會在途中相遇,這類題型就把它稱為相遇問題。相遇問題是研究速度,時間和路程三者數量之間關係的問題。它和一般的行程問題區別在:不是一個物體的運動,所以,它研究的速度包含兩個物體的速度,也就是速度和。
基本公式
相遇問題的關係式是:速度和×相遇時間=路程;路程÷速度和=相遇時間;路程÷相遇時間=速度和。
【解題思路和方法】簡單的題目可直接利用公式,複雜的題目變通後再利用公式。]
例題
例一
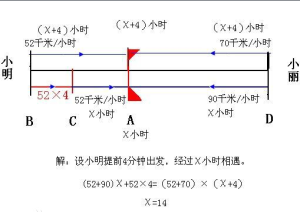 相遇問題
相遇問題 解392÷(28+21)=8(小時)
答:經過8小時兩船相遇。
例二
小李和小劉在周長為400米的環形跑道上跑步,小李每秒鐘跑5米,小劉每秒鐘跑3米,他們從同一地點同時出發,反向而跑,那么,二人從出發到第二次相遇需多長時間?
解“第二次相遇”可以理解為二人跑了兩圈。因此總路程為400×2
相遇時間=(400×2)÷(5+3)=100(秒)
答:二人從出發到第二次相遇需100秒時間。
例三
甲乙二人同時從兩地騎腳踏車相向而行,甲每小時行15千米,乙每小時行13千米,兩人在距中點3千米處相遇,求兩地的距離。
解“兩人在距中點3千米處相遇”是正確理解本題題意的關鍵。從題中可知甲騎得快,乙騎得慢,甲過了中點3千米,乙距中點3千米,就是說甲比乙多走的路程是(3×2)千米,因此,
相遇時間=(3×2)÷(15-13)=3(小時)
兩地距離=(15+13)×3=84(千米)
答:兩地距離是84千米。
注意問題
解答這類問題,要弄清題意,按照題意畫出線段圖,分析各數量之間的關係,選擇解答方法.。相遇問題除了要弄清路程,速度與相遇時間外,在審題時還要注意一些重要的問題:是否是同時出發,如果題目中有誰先出發,就把先行的路程去掉,找到同時行的路程。駛的方向,是相向,同向還是背向。不同的方向解題方法就不一樣。是否相遇。有的題目行駛的物體並沒有相遇,要把相距的路程去掉;有的題目是兩者錯過,要把多行的路程加上,得到同時行駛的路程。

