公式
追及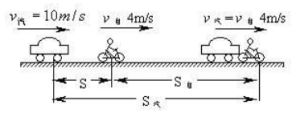 1
1速度差×追及時間=路程差
路程差÷速度差=追及時間(同向追及)
速度差=路程差÷追及時間
甲經過路程—乙經過路程=追及時相差的路程
基本形式:
A.勻加速直線運動的物體追勻速直線運動的物體
這種情況只能追上一次兩者追上前有最大距離,條件:v加=v勻
B.勻減速直線運動追及勻速運動的物體
當v減=v勻時兩者仍沒達到同一位置,則不能追上
當v減=v勻時兩者在同一位置,則恰好能追上,也是兩者避免相撞的臨界條件
當兩者到達同一位置時,v減>v勻,則有兩次相遇的機會
C.勻速運動的物體追及勻加速直線運動的物體
當兩者到達同一位置前,就有v加=v勻,則不能追及.
當兩者到達同一位置時,v加=v勻,則只能相遇一次.
當兩者到達同一位置時,v加<v勻,則有兩次相遇的機會.
D.勻速運動的物體追及勻減速直線運動的物體,這種情況一定能追上.
E.勻加速運動的物體追及勻減速直線運動的物體,這種情況一定能追上.
F.勻減速運動的物體追及勻加速直線運動的物體.
當兩者到達同一位置前,v減=v加,則不能追及.
當v減=v加時兩者恰好到達同一位置,則只能相遇一次.
當第一次相遇時v減<v加,則有兩次相遇的機會.
相遇
相遇路程÷速度和=相遇時間
速度和×相遇時間=相遇路程
相遇路程÷相遇時間=速度和
甲走的路程+乙走的路程=總路程
注意:兩個運動的物體相遇,即相對同一參考系來說它們的位移相等.在解題中一定要注意相遇時間小於運動的總時間.
例題
例:甲、乙同時起跑,繞300米的環行跑道跑,甲每秒跑6米,乙每秒跑4米,
第二次追上乙時,甲跑了幾圈?
基本等量關係:追及時間×速度差=追及距離
本題速度差為:6-4=2(米/每秒)。
甲第一次追上乙後,追及距離是環形跑道的周長300米。
第一次追上後,兩人又可以看作是同時同地起跑,因此第二次追及的問題,就轉化為類似於求解第一次追及的問題。
甲第一次追上乙的時間是:300÷2=150(秒)
甲第一次追上乙跑了:6×150=900(米)
這表明甲是在出發點上追上乙的,因此,第二次追上問題可以簡化為把第一次追上時所跑的距離乘二即可,得
甲第二次追上乙共跑了:900+900=1800(米)
那么甲跑了1800÷300=6(圈)
問題解法
解追及問題的常規方法是根據位移相等來列方程,勻變速直線運動位移公式是一個一元二次方程,所以解直線運動問題中常要用到二次三項式(y=ax2+bx+c)的性質和判別式(△=b²-4ac)。另外,在有兩個(或幾個)物體運動時,常取其中一個物體為參照物,即讓它變為“靜止”的,只有另一個(或另幾個)物體在運動。這樣,研究過程就簡化了,所以追及問題也常變換參照物的方法來解。這時先要確定其他物體相對參照物的初速度和相對它的加速度,才能確定其他物體的運動情況
追及問題,比較實用的應該是方程,這種可以解決所有的問題,我想,算數不是解決追及問題的好方法,應該學會用方程來解。
相關問題
1.A、B、C三個站點位於同一直線上,B站到A、C兩站的距離相等,甲、乙二人分別從A、C兩站同時出發相向而行,甲在距離B站100米處與乙相遇,相遇後兩人繼續前進,甲到達C站後立即返回,經過B站300米又追上乙。問A、C兩站的距離是多少米?2.高速公路上,一輛長4m、速度為110km/h的轎車準備超越一輛長12m、速度為100km/h的卡車。估計轎車從開始追及到完全超越卡車,大約需要多少小時?
3.小王、小李同時從學校去公園,小王每小時行10km,小李有事晚出發,為了能和小王同時到達,小李每小時用12km的速度前行,但小王在行進到路程的2/3時,速度每小時減慢了2km,結果在離公園2km處被小李追上,求學校到公園的距離及小李晚出發了多長時間?
4.甲、乙、丙三人每分鐘的速度分別為30M、40M、50M,甲、乙在A地同時同向出發,丙從B地同時去追趕甲、乙,並追上甲以後又經過十分鐘才追上乙,A、B兩地相距多少米?
5.一條街上,一個騎車人與一個步行人同向而行,騎車人的速度是步行人的3倍,每隔10分鐘有一輛公共汽車超過行人,每隔20分鐘有一輛公共汽車超過騎車人,如果公共汽車從始發站每次間隔同樣的時間發一輛車,那么間隔多少分發一輛公共汽車?
6.列車從甲站到乙站正常行駛速度為60km/h。某次列車從甲站出發時晚點8分鐘,司機把車速提高到80km/h,結果提前2分鐘到達驛站。那么如果按照正常行駛速度來行駛,列車從甲站到乙站要多久呢?

