相對論電動力學
正文
相對論性粒子的電動力學。它採用經典的方法來研究帶電的相對論性粒子與電磁場的相互作用,研究粒子在電磁場中的運動和對場的激發。這裡所謂的相對論性粒子是指其速度接近真空中光速c,因而其運動不服從牛頓方程而必須用相對論力學方程來處理的粒子。相對論電動力學主要套用於高能加速器以及高能電子學中,在高能天體物理等其他學科中也有套用。相對論電動力學的基本方程是麥克斯韋方程組、洛倫茲力公式(見經典電動力學)以及粒子的相對論力學方程,即
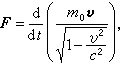 (1)
(1)
相對論性粒子的特點表現在許多方面。例如,通常同號電荷間的排斥作用會使得粒子束逐漸散開,但在高速粒子的情況,一方面由於從粒子發出的電力線集中在與速度垂直的面附近(見運動帶電粒子的電磁場),而在此區域,粒子間的電場作用與磁場作用在很大程度上相互抵消;另一方面,由於高速粒子的質量有極大的增加,因此相對論粒子束的散開效應大大降低。在有些情況(如電子直線加速器中)甚至可以忽略不計。這一結果對高能加速器、高能電子學器件甚至受控熱核反應裝置都有重要意義。又如在回旋加速器中,粒子的迴轉頻率為
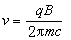 , (2)
, (2)
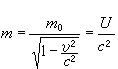 ,其中U為粒子的能量(包括靜質量所相應的能量在內)。這樣隨著粒子能量U的增加,迴轉頻率將減小。要使交變電源與粒子的迴轉同步,有兩種方法,或者使電源頻率也隨之逐漸減小,或者使磁感應強度B隨著軌道半徑增大而增加。相對論性粒子的輻射率也有它的特點。對於直線加速的帶電粒子,輻射率為
,其中U為粒子的能量(包括靜質量所相應的能量在內)。這樣隨著粒子能量U的增加,迴轉頻率將減小。要使交變電源與粒子的迴轉同步,有兩種方法,或者使電源頻率也隨之逐漸減小,或者使磁感應強度B隨著軌道半徑增大而增加。相對論性粒子的輻射率也有它的特點。對於直線加速的帶電粒子,輻射率為 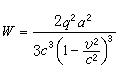 , (3)
, (3)
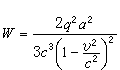 。 (4)
。 (4)
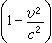 的因子。可是實際上,在高能直線加速器中,輻射損失一般可忽略,而在高能同步加速器或電子加速器中(軌道都是圓形),輻射損失卻可能十分嚴重。這是因為對於作直線運動的相對論性粒子,即使能量增加率較大,相應的ɑ也很小。式(3)通過相對論力學方程可以化為
的因子。可是實際上,在高能直線加速器中,輻射損失一般可忽略,而在高能同步加速器或電子加速器中(軌道都是圓形),輻射損失卻可能十分嚴重。這是因為對於作直線運動的相對論性粒子,即使能量增加率較大,相應的ɑ也很小。式(3)通過相對論力學方程可以化為 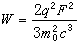 。 (5)
。 (5)
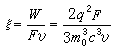 , (6)
, (6)
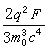 。對於實際採用的 F,這個值是很小的。在圓形軌道情況下,由於向心加速度趨於一個有限值
。對於實際採用的 F,這個值是很小的。在圓形軌道情況下,由於向心加速度趨於一個有限值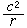 ,故相應的輻射率為
,故相應的輻射率為 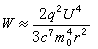 , (7)
, (7)
在加速器中,相對論電動力學還用來研究注入粒子的成束率、束流的聚焦及其運動的穩定性、粒子的能譜分布等重要問題。當束流強到一定程度時,還要研究束流對真空匣和腔體內電磁場的激發以及這種激發場對束流的反作用等。
相對論電動力學的另一重要套用是高能電子學。值得提出的是70年代在迴旋管研究上的成就。它解決了產生大功率亞毫米波段的微波問題。
在迴旋管中,在強磁場中作迴旋運動的相對論性電子束將與微波相互作用(當磁場足夠強時,電子的迴旋頻率可達到亞毫米波的頻段)。利用相對論電子的迴旋頻率隨著電子能量的減少而增加的效應,適當調諧微波,可使電子束不斷地向微波放出能量,從而得到大功率的亞毫米波的輸出(相應於回旋加速器的反過程)。這一成功是微波電子學的一項重大突破,它填補了從毫米波到紅外射線之間的間隙。