運動帶電粒子的電磁場
正文
微觀帶電粒子在運動中所產生的電磁場。這個問題雖然已經超出經典電動力學的範圍,但經典理論仍有一定的意義。因為在某些情況下,量子效應並不重要,經典理論的結果仍近似正確,可以在實踐中直接套用(例如計算高溫電漿或加速器中粒子的輻射);還有一些情況,量子效應雖然顯著,但經典結果可按一定方式與量子理論的結果相對應;另外,通過經典理論結果與量子理論結果間的對比,可以更好地認識量子效應的特點。在經典理論中,通常把帶電粒子當作一個線度極小的帶電體,且一般不考慮它的自旋磁矩。這時一個作任意運動的帶電粒子所產生的電磁勢用高斯單位制可表示為

 通常稱為都卜勒因子。
通常稱為都卜勒因子。 從李納-維謝爾勢,可以計算出任意運動的帶電粒子的電磁場,結果為

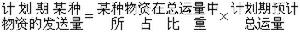 。此項對輻射沒有貢獻,代表依附於帶電粒子的那一部分場,有時稱為粒子的自場。在粒子靜止的情況,自場就化為通常的庫侖場。第二項不僅與t*時刻粒子的位置和速度有關,還正比於粒子在t*時刻的加速度。此項電場和磁場
。此項對輻射沒有貢獻,代表依附於帶電粒子的那一部分場,有時稱為粒子的自場。在粒子靜止的情況,自場就化為通常的庫侖場。第二項不僅與t*時刻粒子的位置和速度有關,還正比於粒子在t*時刻的加速度。此項電場和磁場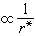 ,E和B大小相等,而且E、B和r*三者互相垂直。所對應的能流就在r*方向,其數值
,E和B大小相等,而且E、B和r*三者互相垂直。所對應的能流就在r*方向,其數值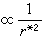 ,這表明此項代表粒子的輻射場。以上特點顯示了輻射場的橫波性。
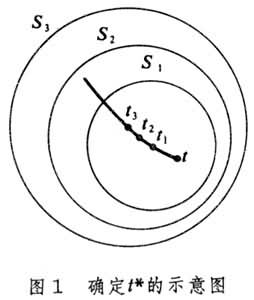
,這表明此項代表粒子的輻射場。以上特點顯示了輻射場的橫波性。 上面所述的t*可以採用下述圖解法來確定:在粒子所經歷的軌道上(直到t時刻為止)取一系列的點,它們分別相應於粒子在t1、t2、t3……時刻的位置,如圖1所示。然後以這些點為中心,分別以с(t-t1)、с(t-t2)、с(t-t3)……為半徑畫出一系列的球面S1、S2、S3……。從電磁影響傳播速度為с即可看出:粒子在ti時刻所產生的電磁影響,到t時刻正好傳到Si面上。因此Si面上t時刻的電磁勢和場強應由ti時刻粒子的狀態所決定。於是對於球面Si上的點來說,與t時刻相應的t*即為ti,r*即為球心到該點的矢徑。
 運動帶電粒子的電磁場
運動帶電粒子的電磁場對於非相對論粒子,
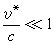 ,輻射場強可近似為
,輻射場強可近似為 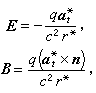
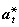
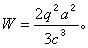
上式通常稱為拉莫爾輻射功率公式。如果用p表示粒子對任一固定點的電偶極矩,則
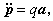
其中
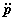 表示p對時間的兩次微商,於是低速(非相對論)粒子的輻射場可表為
表示p對時間的兩次微商,於是低速(非相對論)粒子的輻射場可表為 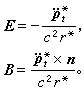
輻射功率為
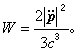
由此可見,低速運動粒子的輻射相應於電偶極輻射。
對於帶電粒子作等速運動的簡單情況,v等於常矢量v0。這時E 和B可以通過即時的r(從t時刻粒子位置到場點的距離)表示出來。結果為
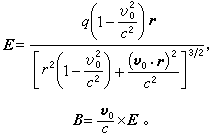
 運動帶電粒子的電磁場
運動帶電粒子的電磁場對於非相對論粒子,
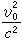 與1相比可以略去,這時
與1相比可以略去,這時 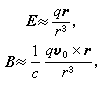
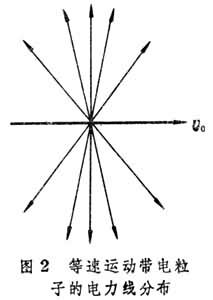
當速度接近於с時,電磁場差不多集中在通過帶電粒子並且垂直於v0的平面上,形成為一薄片形的分布。
關於速度很高而又有加速度的粒子的輻射,可參見軔致輻射、回旋加速器輻射和同步加速器輻射。
