概念
相對同倫是同倫群的推廣。若(X,A,x)是有基點的空間偶,定義:
P(X;x,A)=(X,A,x)
是X中以x為始點,終點在A中的所有道路的空間,帶有緊開拓撲,則有自然的連續映射π:P(X;x,A)→A,定義如下:對於ω∈P(X,x,A),π(ω)=ω(1).若n≥1是整數,則(X,A,x)的第n個相對同倫集π(X,A,x)定義為:
π(X,A,x)=π(Ω(P(X;x,A)),ω),
其中Ω是定義在有基點的拓撲空間範疇上的閉路函子,π(Ω(P(X;x,A)),ω)是Ω(P(X;x,A))中包含常值閉路ω的道路連通分支作為基點的所有道路連通分支的集合。由函子Ω的性質可知,π(X,A,x)=π(P(X;x,A),ω)。對於n≥2,π(X,A,x)是一個群;;對於n≥3,它是一個交換群;對於一切n≥1,π是定義在有基點的拓撲空間偶上的一個函子。若f:(X,A,x)→(Y,B,y)是空間偶之間的保基點連續映射,則記:
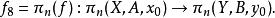 相對同倫
相對同倫相對同倫有一些與相對同調相類似的性質,例如,相對同倫的正契約倫序列等。
同倫
設f、g是拓撲空間X到Y的兩個連續映射,若存在連續映射H:X×I→Y使得:
H(x,0)=f(x)
H(x,1)=gx∈X
則稱f與g同倫,記為f≃g:X→Y或f≃g,映射H稱為f與g之間的一個同倫。f與g的同倫H也可理解為單參數映射族{h},h連續地依賴於t且h=f,h=g,即當參數t從0變到1時,映射f連續地形變為g。與常值映射同倫的映射稱為零倫的。若以C[X,Y]表示X到Y的一切連續映射之集,則同倫關係≃是C[X,Y]上等價關係,每個等價類稱為一個同倫類,同倫類的全體所成集記為[X,Y]。設Y是R的子空間,f,g:X→Y是連續映射,若對每個x∈X,點f(x)與g(x)可由Y中線段連結,則f≃g:X→Y,若Y是R中凸集,任何映射f:X→Y都零倫,即[X,Y]僅含一個元素。設X,Y與Z均為拓撲空間,若f≃f:X→Y,g≃g: Y→Z,則gf≃gf: X→Z。
設X,Y為拓撲空間,若存在連續映射f:X→Y和g:Y→X,使得gf≃Id且f·g≃id。這Id、id均表示恆同映射,則稱f為同倫等價,g為f的同倫逆,而將X與Y稱為具有相同的倫型,或簡稱同倫的,記作X≃Y。與單點空間同倫的空間稱為可縮的,或者存在x∈X,使得常值映射C:X→X。x→x與映射id同倫,空間X可縮。R和R中凸集均為可縮空間。同倫關係是拓撲空間之間的等價關係。X可縮等價於下列幾條中任意一條:(1)id≃0,即恆同映射id零倫。(2) 對任意空間Y,映射f:X→Y,有f≃0。(3)對任意空間Z和連續映射g:Z→X,g≃0。
設A是空間X的子空間,i:A→X表包含映射,若存在連續映射r:X→A,使得r|=id(或r·i=id),則r稱為X到A的保核收縮,A稱為X的收縮核。若有保核收縮r:X→A滿足i·rid:X→X,則H稱為X到A的形變收縮,A稱為X的形變收縮核,若同倫H還滿足對任意x∈A和t∈I有H(x,t)=x,則H稱為X到A的一個強形變收縮,A稱為X的強形變收縮核。強形變收縮是形變收縮,且若A是X的形變收縮核,則內射i:A→X是同倫等價。
兩個拓撲空間X和Y同倫等價的充要條件是:存在空間Z,使得X與Y分別同胚於Z的兩個強形變收縮核。
倫型相同的拓撲空間所共有的性質稱為同倫不變數。由於同胚的空間必同倫,故同倫不變數一定是拓撲不變數。代數拓撲學主要研究空間的同倫。
同倫群
同倫群(homotopy groups)是基本群的高維推廣。基本群是從單位閉區間I到拓撲空間X的閉路的同倫等價類和其運算得到的。考慮n維歐氏空間R中的n維方體:
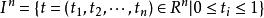 相對同倫
相對同倫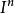 相對同倫
相對同倫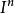 相對同倫
相對同倫是的邊界,即:
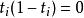 相對同倫
相對同倫存在i使得,
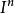 相對同倫
相對同倫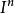 相對同倫
相對同倫設X為拓撲空間,x∈X,用M(X,x)表示全體連續映射α:(,)→(X,x)所成的集合,α和α′相對於I的同倫關係αα′是M(X,x)上的一個等價關係,它把M(X,x)的元素分成一些同倫等價類,用π(X,x)表示這些等價類所成的集合.定義映射α*β:(I,I)→(X,x),使得:
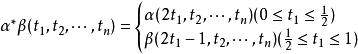 相對同倫
相對同倫從而,α*β∈M(X,x),並且,若α∽α′,β∽β′,則:
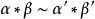 相對同倫
相對同倫因此,可在π(X,x)中定義運算:
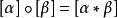 相對同倫
相對同倫並且關於這一運算使它構成群,仍記為π(X,x),稱為拓撲空間X的以x為基點的n維同倫群。1維同倫群就是基本群π(X,x).同倫群還有一種等價定義方式,它是用n維球面S代替n維方體I,這種定義給討論同倫群的性質有時帶來方便。類似基本群的討論,同倫群具有性質:當拓撲空間是道路連通空間時,其同倫群與基點選取無關;利用連續映射誘導的同倫群之間同態的一些性質得出,同倫群是同倫型不變數(更是拓撲不變的);當n≥2時,同倫群π(X,x)是交換群,因而有時把運算寫成[α]+[β]。同倫群與同調群的一些基本關係:對於連通復形K的多面體|K|,1維同調群同構於基本群的交換化,即:
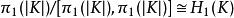 相對同倫
相對同倫這裡[π(|K|),π(|K|)]表示基本群π(|K|)的換位子群。高維同倫群與同調群之間的關係,由赫萊維茨(Hurewicz,W.)的同構定理給出:設|K|是連通復形K的多面體,當n≥2時,若|K|的1,2,…,n-1維同倫群都是平凡群,則π(|K|)xH(K)。
