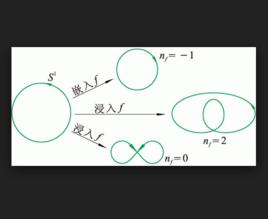
描述
在同倫變換下保持不變的性質,就稱為同倫不變數。 比如虧格(洞眼的個數),歐拉示性數等等。但是維數就不是同倫不變數。
拓撲學家中流傳著這么一句俏皮話:“一個拓撲學家分不清麵包圈和咖啡杯的差別。”這是因為兩者是同倫的,即麵包圈可以連續形變成咖啡杯。在施瓦辛格主演的科幻電影《終結者2》裡面那個液態機器人殺手,它的每次變化都可以視為同倫變換。 但那次被施瓦性格用槍打爆腦袋不能算同倫變化, 因為這不是連續地形變。同倫是關於映射的等價關係,同倫等價才是關於空間的等價關係。最後舉的兩個例子更適合在同胚的概念中提及,在此處提雖然從邏輯上講沒錯,但也容易讓初學者混淆。 建議舉不同倫的例子如下:兩個映射,一個是圓周到自身的恆同映射,另一個則是自變數在圓周上轉一圈時相應的映射的值在圓周上轉兩圈。舉同倫等價的例子如下:“日”字和“8”字。
產生
同倫和倫移的定義由brouwer於1911年給出,雖然它的直觀的觀念形變(deformation)早在lagrange時代的變分學中已經出現並被使用,或許還可以追溯到更早。
函式的同倫
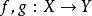 同倫
同倫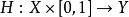 同倫
同倫給定兩個拓撲空間X和Y。考慮兩個連續函式,若存在一個 連續映射使得
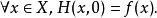 同倫
同倫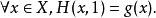 同倫
同倫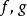 同倫
同倫則稱(在Y里)同倫。
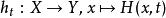 同倫
同倫換言之:每個參數 t對應到一個函式;隨著參數值t從 0 到 1 變化,H連續地從f變化到g。
 同倫
同倫另一種觀點是:對每個,函式H 定義一條連線f(x) 與g(x)的路徑:
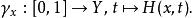 同倫
同倫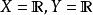 同倫
同倫例一:取, f(x)=1及g(x)=-1。則f與 g透過下述函式在Y中同倫。
H(x,t)=1-2t(注意到此例子不依賴於變數x,通常並非如此。)
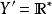 同倫
同倫注:“在Y中同倫”的說法提示一個重點:在例一中若將Y=R代為子空間,則雖然f與g仍取值在Y,但此時它們並不同倫。此點可藉中間值定理驗證。
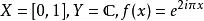 同倫
同倫例二:取及g(x)=0。f描繪一個以原點為圓心之單位圓;g停在原點。f與g透過下述連續函式同倫:
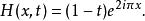 同倫
同倫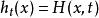 同倫
同倫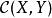 同倫
同倫幾何上來看,對每個值t,函式描繪一個以原點為圓心,半徑1-t的圓。函式間的同倫是(即從 X 到 Y 全體連續函式的集合)上的等價關係。同倫的初步套用之一,是藉由環路的同倫定義何謂單連通。
相對同倫
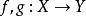 同倫
同倫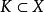 同倫
同倫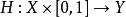 同倫
同倫為定義高階基本群,必須考慮相對於一個 子空間的同倫概念。這是指能在不變動該子空間的狀況下連續變化,正式定義是:設是連續函式,固定子空間;若存在前述同倫映射,滿足:
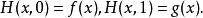 同倫
同倫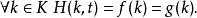 同倫
同倫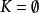 同倫
同倫則稱 f,g 相對於K 同倫。若取,則回到原先的同倫定義。
空間同倫等價
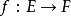 同倫
同倫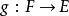 同倫
同倫給定兩個拓撲空間E 與F,我們稱之 同倫等價(或稱具 相同倫型),若且唯若存在兩個連續映射與,使得:
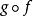 同倫
同倫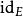 同倫
同倫同倫到E 的恆等映射。
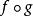 同倫
同倫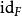 同倫
同倫同倫到F的恆等映射。
同胚蘊含同倫,反之則不然,詳見以下例子:
例三:
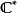 同倫
同倫一個平面上的圓或橢圓同倫等價到,即去掉一點的平面。線段[a,b]、閉圓盤及閉球間兩兩同倫等價,它們皆同倫等價於一個點。
同倫等價是個拓撲空間之間的等價關係。許多代數拓撲學裡的性質均在同倫等價下不變,包括有:單連通、同調群及上同調群等等。
同痕
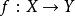 同倫
同倫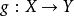 同倫
同倫同痕是同倫的加細版;我們進一步要求所論的函式和是嵌入,並要求兩者間可用一族嵌入映射相連。
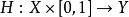 同倫
同倫定義: f與 g被稱為同痕的,若且唯若存在 連續映射使之滿足:
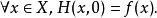 同倫
同倫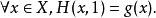 同倫
同倫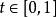 同倫
同倫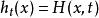 同倫
同倫對所有,映射是個嵌入映射。
同痕的概念在紐結理論中格外重要:若兩個結同痕,則我們視之相等;換言之,可以在不使結扯斷或相交的條件下彼此連續地變形。