定義
A和B中至少有一件事情發生：A∪B； A與B同時發生：A∩B，AB，如果P(A B) =P(A) P(B)，稱A,B 相互獨立。
性質
相互獨立事件（1）A,B獨立等價於
獨立，其中
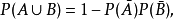相互獨立事件(2)A,B獨立,則
是A的對立事件。
與集合的關係
集合相交相互獨立事件其實沒有明確的相交與互斥關係。因為相交就意味著事件相互影響，互斥意味著事件不可能同時發生；而相互獨立事件既有可能同時發生，也有可能不同時發生，那么它們到底是什麼關係呢？其實這就是機率問題，可能同時發生，也有可能不同時發生，這和物理中的波粒二象性有些類似，如果一定要畫圖像，它們的圖像就是動態的。
（2014年1月8日 zb9006 編輯）：上述一段論述有誤。相互獨立事件之間沒有相互的影響，故其中一個事件的發生不影響另一個事件的發生機率，則必然存在兩個事件同時發生的可能性（除非有一個事件機率為0），實際上，相互獨立事件是有相交關係的事件間關係的特例。相互獨立事件間必然有P（A I B）= P（A）及P（B I A）= P（B），關於這一點可以這么理解：P（A I B）是事件B發生後事件A發生的機率，通常的計算是P（AB）÷ P（B），實際意義是事件A和事件B同時發生的可能性在事件B發生（包含事件A同時發生的情況）的可能性中占的比率（即在事件B的範圍內事件A的發生機率），由於A和B相互獨立，事件B的發生不對事件A的發生造成影響，即在事件B的範圍內事件A的發生機率和整個樣本空間中事件A發生的機率一樣，所以有P（A I B）= P（A）和 P（B I A）= P（B）。
推導
相互獨立事件的公式由條件機率推得：以任意兩事件AB為例
P(AB)=P(A)P(B|A)或P(AB)=P(B)P(A|B)
P(B|A)表示A發生的條件下B發生的機率。所以，當AB相互獨立時，P(B|A)=P（B）
推廣到n個任意事件A1、A2、A3……An
P（A1A2A3……An）=P(A1)*P(A2|A1)*P(A3|A1A2)*P(A4|A1A2A3)*……*P(An|A1A2A3……A(n-1））
註：P(A4|A1A2A3)表示A1A2A3同時發生的條件下A4發生的機率
當A1A2A3……An相互獨立P（A1A2A3……An）=P(A1)*P(A2)*P(A3)*P(A4)*……*P(An)
如：A、B、C為事件，P（ABC）>0，則P（AB|C）=P（A|C）*P（B|C）充要條件是P（B|AC）*P（B|AC）。
