函式介紹
在自然科學領域中, 皮爾遜相關係數廣泛用於度量兩個變數之間的相關程度,其值介於-1與1之間。它是由卡爾·皮爾遜從弗朗西斯·高爾頓在19世紀80年代提出的一個相似卻又稍有不同的想法演變而來的。這個相關係數也稱作“皮爾遜積矩相關係數”。
 圖1.皮爾遜相關係數舉例
圖1.皮爾遜相關係數舉例 皮爾遜相關係數
皮爾遜相關係數 皮爾遜相關係數
皮爾遜相關係數 皮爾遜相關係數
皮爾遜相關係數 皮爾遜相關係數
皮爾遜相關係數圖1中,幾組的點集,以及各個點集中和之間的相關係數。我們可以發現相關係數反映的是變數之間的線性關係和相關性的方向(第一排),而不是相關性的斜率(中間),也不是各種非線性關係(第三排)。請注意:中間的圖中斜率為0,但相關係數是沒有意義的,因為此時變數是0。
定義
兩個變數之間的皮爾遜相關係數定義為兩個變數之間的協方差和標準差的商:
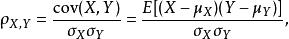 皮爾遜相關係數
皮爾遜相關係數 皮爾遜相關係數
皮爾遜相關係數 皮爾遜相關係數
皮爾遜相關係數上式定義了 總體相關係數,常用希臘小寫字母作為代表符號。估算樣本的協方差和標準差,可得到 皮爾遜相關係數,常用英文小寫字母 代表:
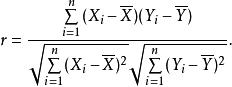 皮爾遜相關係數
皮爾遜相關係數 皮爾遜相關係數
皮爾遜相關係數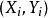 皮爾遜相關係數
皮爾遜相關係數亦可由 樣本點的標準分數均值估計,得到與上式等價的表達式:
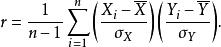 皮爾遜相關係數
皮爾遜相關係數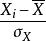 皮爾遜相關係數
皮爾遜相關係數 皮爾遜相關係數
皮爾遜相關係數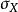 皮爾遜相關係數
皮爾遜相關係數 皮爾遜相關係數
皮爾遜相關係數其中 、 及 分別是對 樣本的標準分數、樣本平均值和樣本標準差。
數學特性
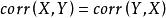 皮爾遜相關係數
皮爾遜相關係數總體和樣本皮爾遜係數的絕對值小於或等於1。如果樣本數據點精確的落在直線上(計算樣本皮爾遜係數的情況),或者雙變數分布完全在直線上(計算總體皮爾遜係數的情況),則相關係數等於1或-1。皮爾遜係數是對稱的: 。
 皮爾遜相關係數
皮爾遜相關係數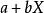 皮爾遜相關係數
皮爾遜相關係數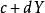 皮爾遜相關係數
皮爾遜相關係數皮爾遜相關係數有一個重要的數學特性是,因兩個變數的位置和尺度的變化並不會引起該係數的改變,即它該變化的不變數(由符號確定)。也就是說,我們如果把移動到和把Y移動到,其中a、b、c和d是常數,並不會改變兩個變數的相關係數(該結論在總體和樣本皮爾遜相關係數中都成立)。我們發現更一般的線性變換則會改變相關係數:
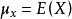 皮爾遜相關係數
皮爾遜相關係數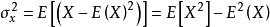 皮爾遜相關係數
皮爾遜相關係數 皮爾遜相關係數
皮爾遜相關係數由於 , , 也類似, 並且
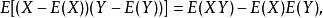 皮爾遜相關係數
皮爾遜相關係數故相關係數也可以表示成
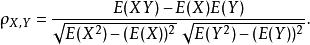 皮爾遜相關係數
皮爾遜相關係數對於樣本皮爾遜相關係數:
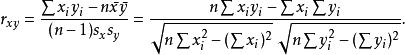 皮爾遜相關係數
皮爾遜相關係數以上方程給出了計算樣本皮爾遜相關係數簡單的單流程算法,但是其依賴於涉及到的數據,有時它可能是數值不穩定的。
解釋
 皮爾遜相關係數
皮爾遜相關係數 皮爾遜相關係數
皮爾遜相關係數 皮爾遜相關係數
皮爾遜相關係數 皮爾遜相關係數
皮爾遜相關係數皮爾遜相關係數的變化範圍為-1到1。 係數的值為1意味著 X和 Y可以很好的由直線方程來描述,所有的數據點都很好的落在一條直線上,且隨著 的增加而增加。係數的值為−1意味著所有的數據點都落在直線上,且隨著 的增加而減少。係數的值為0意味著兩個變數之間沒有線性關係。
 皮爾遜相關係數
皮爾遜相關係數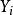 皮爾遜相關係數
皮爾遜相關係數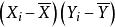 皮爾遜相關係數
皮爾遜相關係數 皮爾遜相關係數
皮爾遜相關係數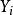 皮爾遜相關係數
皮爾遜相關係數 皮爾遜相關係數
皮爾遜相關係數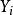 皮爾遜相關係數
皮爾遜相關係數更一般的, 我們發現,若且唯若 和 均落在他們各自的均值的同一側, 則 的值為正。 也就是說,如果 和 同時趨向於大於,或同時趨向於小於他們各自的均值,則相關係數為正。 如果 和 趨向於落在他們均值的相反一側,則相關係數為負。
1.幾何學的解釋
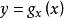 皮爾遜相關係數
皮爾遜相關係數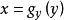 皮爾遜相關係數
皮爾遜相關係數對於沒有中心化的數據, 相關係數與兩條可能的回歸線和夾角的餘弦值一致。
 皮爾遜相關係數
皮爾遜相關係數對於中心化過的數據 (也就是說, 數據移動一個樣本平均值以使其均值為0), 相關係數也可以被視作由兩個隨機變數向量夾角的餘弦值。
一些人傾向於是用非中心化的相關係數, 比較如下:
例如,有5個國家的國民生產總值分別為 10, 20, 30, 50 和 80 億美元。 假設這5個國家 (順序相同) 的貧困百分比分別為 11%, 12%, 13%, 15%, and 18% 。 令 x和 y分別為包含上述5個數據的向量: x= (1, 2, 3, 5, 8) 和 y= (0.11, 0.12, 0.13, 0.15, 0.18)。
 皮爾遜相關係數
皮爾遜相關係數利用通常的方法計算兩個向量之間的夾角,未中心化的相關係數是:
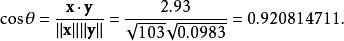 皮爾遜相關係數
皮爾遜相關係數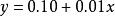 皮爾遜相關係數
皮爾遜相關係數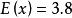 皮爾遜相關係數
皮爾遜相關係數 皮爾遜相關係數
皮爾遜相關係數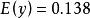 皮爾遜相關係數
皮爾遜相關係數 皮爾遜相關係數
皮爾遜相關係數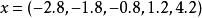 皮爾遜相關係數
皮爾遜相關係數 皮爾遜相關係數
皮爾遜相關係數我們發現以上的數據特意選定為完全相關:。 於是,皮爾遜相關係數應該等於1。將數據中心化 (通過移動和通過移動) 得到和從中,
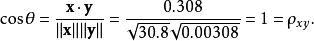 皮爾遜相關係數
皮爾遜相關係數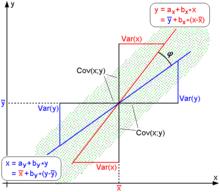 圖2.幾何解釋——皮爾遜相關係數
圖2.幾何解釋——皮爾遜相關係數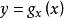 皮爾遜相關係數
皮爾遜相關係數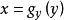 皮爾遜相關係數
皮爾遜相關係數說明:圖2中,回歸直線: [紅色] 和 [藍色]
2.皮爾遜距離
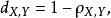 皮爾遜相關係數
皮爾遜相關係數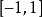 皮爾遜相關係數
皮爾遜相關係數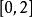 皮爾遜相關係數
皮爾遜相關係數皮爾遜距離度量的是兩個變數X和Y,它可以根據皮爾遜係數定義成我們可以發現,皮爾遜係數落在,而皮爾遜距離落在。
分析
 皮爾遜相關係數
皮爾遜相關係數 皮爾遜相關係數
皮爾遜相關係數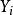 皮爾遜相關係數
皮爾遜相關係數樣本相關係數的平方, 亦稱作coefficient of determination, 利用簡單線性回歸估計由引起的的變化。 一開始,圍繞它們平均值上的變化可以分解成
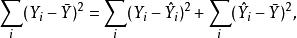 皮爾遜相關係數
皮爾遜相關係數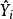 皮爾遜相關係數
皮爾遜相關係數其中 是作回歸分析時的適應值。 整理後得
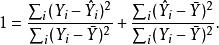 皮爾遜相關係數
皮爾遜相關係數 皮爾遜相關係數
皮爾遜相關係數 皮爾遜相關係數
皮爾遜相關係數 皮爾遜相關係數
皮爾遜相關係數兩個被加數是由(右邊)引起的的變化和不是由(左邊) 引起的變化。
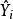 皮爾遜相關係數
皮爾遜相關係數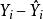 皮爾遜相關係數
皮爾遜相關係數接下來, 我們利用最小方差回歸模型, 使和 的樣本協方差為0。 於是,觀測數據和適應值的樣本相關係數可以被寫成
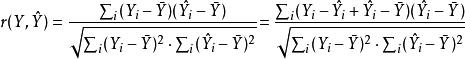 皮爾遜相關係數
皮爾遜相關係數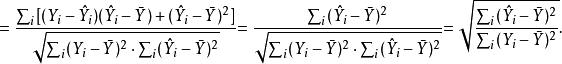 皮爾遜相關係數
皮爾遜相關係數於是
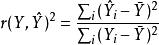 皮爾遜相關係數
皮爾遜相關係數 皮爾遜相關係數
皮爾遜相關係數 皮爾遜相關係數
皮爾遜相關係數是由的線性方程引起的的平均變化。
