基本介紹
統計相關關係按相關因素的多少分類可分為 簡 單相關和 復相關。
簡單相關(simple correlation)也稱 單相關,是指兩個變數之間的相關方向和程度的分析。例如,家庭收入水平和食品支出比重之間的相關關係分析。
復相關(multiple correlation)指兩個以上的變數之間的相關分析。例如,商品購買力與居民貨幣收入、居民非商品支出、手存現金、儲蓄等因素之間的相關關係分析等 。
相關關係的判斷
面對雜亂的社會經濟現象,人們常將其觀察的結果數量化為統計數據,並初步判斷其間的相關關係。這種判斷一般是根據理論或經驗藉助相關表、相關圖等工具進行的,並在此基礎上需要做關係密切程度的測定。
理論與經驗分析
這是對相關事物的關係最為關鍵的分析,如果現象之間的關聯已被前人發現,我們就要參照其總結的規律和經驗,對其進行量化的證實或證偽。如果現象之間確實存在著未被人們認知的客觀聯繫,在數量化的統計資料中必然要顯現出來。經過我們的研究可以總結或升華為經濟理論。
在理論分析中有些現象之間看似密切相關,但其未必具有直接的必然聯繫。如彩色電視機與電冰櫃的銷售量,兩者在一段時間內同時增長,看起來密切相關,能說這兩種現象具有客觀的必然聯繫嗎? 顯然不能。其實,它們都受購買力水平的制約。在購買力水平較高且大幅度增長的條件下,這兩種商品的銷售量才可能同時增長。如果購買力水平較低且增長有限,可能其中的一種商品的銷售量增長,另一種商品的銷售量穩定甚至下降;或者一種商品的銷售量增長快,另一種商品的銷售量出現波動狀態。
可見,理論分析是測定相關關係的前提。由於現象之間的相關關係比較複雜,測定相關關係之前,除了理論分析以外,還要利用相關表和相關圖粗略地判斷現象之間的相關程度和相關形態 。
相關表和相關圖
相關表(correlation table)是反映現象間關係的數據表格,常有簡單表與複雜表之分:一般的簡單相關表是將具有相關關係的兩個變數值按其中一個的大小順序排列,另一個依其對應關係編排而成的統計表。它是粗略觀察現象之間相關程度的一種有效工具,同時也是繪製相關圖和測定相關關係的依據。複雜表是以一個變數順序排列為行標目,而另一個變數的順序排列為列標目,所有的統計數據都在各行和列的交義點上,這樣數據的分布就反映出了相關的大致程度和方向了。
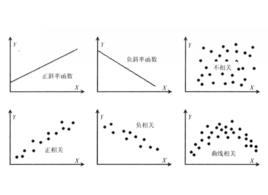
相關圖(correlation graph)也稱相關散點圖,它是將具有相關關係的兩個變數值描繪在坐標圖上。以橫軸表示變數X(常為自變數),縱軸表示變數Y(常為因變數),按兩變數的對應值標出坐標點的分布狀況的統計圖。它是粗略觀察現象之間相關程度和相關形態的一種有效工具,它為測定相關關係奠定有效基礎。如表1所示。
 簡單相關 簡單相關 | 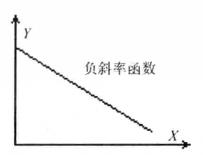 簡單相關 簡單相關 | 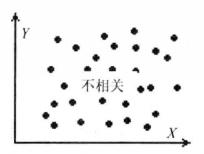 簡單相關 簡單相關 |
 簡單相關 簡單相關 | 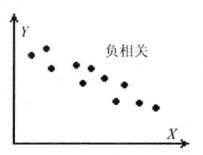 簡單相關 簡單相關 | 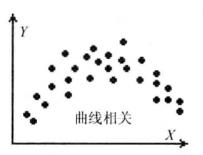 簡單相關 簡單相關 |
相關表和相關圖均具有粗略觀察現象之間相關關係的功能;相關圖與相關表相比較,還有觀察相關形態的作用;但相關圖必須以相關表提供的資料為依據來繪製 。
相關程度的測定
測定線性相關的密切程度的常用方法是 皮爾遜相關係數,現就其主要內容介紹如下:
相關係數的含義
相關係數(correlation coefficient)是皮爾遜相關係數的簡稱,有時也叫簡單相關係數。它是線上性相關的條件下,說明兩個現象之間緊密程度的統計分析指標。
它具有四個特點:
(1) 兩變數為對稱關係(或稱“對等關係”),即可以不區分自變數和因變數;
(2) 相關係數只有一個值,不受自變數和因變數換位的影響;
(3) 相關係數有正負號,反映正相關或負相關;
(4) 若以抽樣調查取得資料,則兩變數均應有相同的隨機性,這也是對稱關係的要求。對全面統計資料而言,不存在隨機性的問題,均為確定性資料。
相關係數的計算方法有若干種,最易理解的一種叫 積差法,直接來源於數理統計中相關係數的定義。相關係數的定義(積差法)為:兩變數的協方差與兩變數各自標準差乘積之比。其相應的定義公式為:
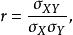 簡單相關
簡單相關 簡單相關
簡單相關 簡單相關
簡單相關 簡單相關
簡單相關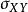 簡單相關
簡單相關式中,代表相關係數;為變數X的標準差;代表變數Y的標準差;代表變數X與Y的協方差。對相關係數進行等價變換,可以得到很多表達式,如:
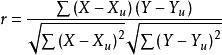 簡單相關
簡單相關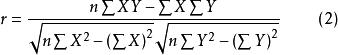 簡單相關
簡單相關 簡單相關
簡單相關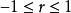 簡單相關
簡單相關表示變數X和Y的線性相關方向和相關程度,取值範圍為。
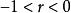 簡單相關
簡單相關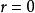 簡單相關
簡單相關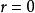 簡單相關
簡單相關當時,相關圖分布呈現出Y隨X的增加而減少的負斜率趨勢,即為負相關;當時,相關圖分布通常呈現出不規則狀態,變數Y不受變數X的影響,表明X和Y之間沒有線性相關關係。但必須注意,,只能說明X與Y之間沒有線性相關關係,而不能隨意排斥其它相關關係,或許存在著某種形態的曲線相關。
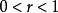 簡單相關
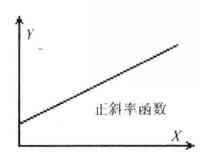
簡單相關當時,相關圖分布呈現出Y隨X 的增加而增加的正斜率趨勢,即為正相關。
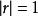 簡單相關
簡單相關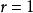 簡單相關
簡單相關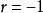 簡單相關
簡單相關當時,相關散點圖呈現在一條直線上,即Y與X完全線性相關。,時,表現為完全正相關;時,表現為完全負相關。
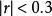 簡單相關
簡單相關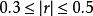 簡單相關
簡單相關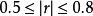 簡單相關
簡單相關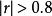 簡單相關
簡單相關為了判斷現象之間相關程度的高低,人們根據經驗一般將社會經濟現象中的相關係數劃分為四個等級:為不相關,為低度相關,,為顯著相關,為高度相關。
相關係數的計算
(1)根據定義或公式先計算式中的各要素,然後用來計算求得相關係數。
(2)利用統計軟體進行計算。使用任何一款統計軟體,都可以直接計算相關係數。
相關係數的檢驗
 簡單相關
簡單相關 簡單相關
簡單相關由於我們在現實的統計中往往只能得到一個樣本,所以根據樣本計算的相關係數就具有一定的隨機性,即與總體相關係數之間有一定的差別。這就需要採用假設檢驗的方法對樣本相關係數的顯著性做出判斷。經英國統計學家費雪做如下變換:
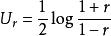 簡單相關
簡單相關和
 簡單相關
簡單相關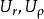 簡單相關
簡單相關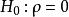 簡單相關
簡單相關這裡的都接近服從常態分配,因此可以利用樣本相關係數估計總體相關係數。即在原假設成立時,具有如下檢驗統計量:
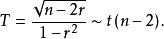 簡單相關
簡單相關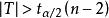 簡單相關
簡單相關即當時,否定原假設 。