函式exp(1/z)，在z=0處具有本性奇點。z的色相表示它的輻角，而發光度則表示絕對值。這個圖像說明了接近於奇點時，可以取得任何非零的值。
皮卡小定理
皮卡定理 皮卡定理皮卡小定理說明，如果函式 是整函式且不是常數，則 的值域或者是整個複平面，或者只去掉一個點。 這個定理在1879年證明。它強化了劉維爾定理：任何不是常數的整函式都一定是無界的。
皮卡的原始證明利用了模函式（Modular lambda function）。
證明概要如下：
皮卡定理 皮卡定理
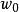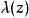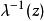皮卡定理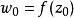
皮卡定理
皮卡定理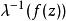
皮卡定理
皮卡定理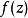
皮卡定理
皮卡定理若 的值域不包含複平面上的兩個點，不失一般性地，可以假設 的值域不包含0和1，設 是其值域中的點，在這個點附近，可以選取模函式 的逆的某個單值解析分支，記作 。利用模函式的通用覆蓋性和單值性定理，可以將 點（ ）附近定義的複合映射 解析延拓到整個複平面上，從而得到一個在複平面上單值解析但有界的函式。根據劉維爾定理，該函式為常函式。因此 也是常函式。
皮卡大定理
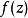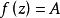皮卡定理
皮卡定理如果 在點w具有本性奇點，那么在任何含有w的開集中，對任意非∞的複數值A，有無窮多個z使得 ，A最多只有一個例外。 以上定理是說，全純函式在本性奇點的任意鄰域內，“無窮多次”地取到每一個有限的復值，至多有一個例外值。 這個定理強化了魏爾施特拉斯-卡索拉蒂定理，它只保證了f的值域在複平面內是稠密的。
性質
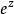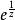皮卡定理
皮卡定理這個“唯一的例外”實際上在兩個定理中都是需要的：指數函式 是一個整函式，永遠不能是零。 在0處具有本性奇點，但仍然不能取得零。
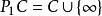皮卡定理
皮卡定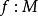理
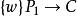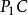皮卡定理
皮卡定理皮卡大定理在一個更一般的形式中也是正確的，可以套用於亞純函式：如果M是一個黎曼曲面，w 是M上的一個點，表示黎曼球面， \是一個全純函式，在w處具有本性奇點，那么在M的任何含有w的開子集中，函式f都可以取得除了兩個點以外的所有的點。
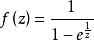皮卡定理例如，亞純函式在z = 0處具有本性奇點，在0的任何鄰域內都無窮多次取得值∞；但它無法取得0或1的值。
皮卡小定理可以從皮卡大定理推出，因為整函式要么是多項式，要么在無窮遠處具有本性奇點。
皮卡定理介紹
皮卡定理是兩個不同的數學定理的泛稱，由法國數學家埃米爾·皮卡證明。這兩個定理都涉及解析函式的值域。
