歷史
這個定理最早由數學家朱塞佩·皮亞諾在1886年發表,但是他給出的證明是錯誤的。1890年他又發表了一個正確的運用逐次逼近法的證明。
定理
 皮亞諾存在性定理
皮亞諾存在性定理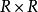 皮亞諾存在性定理
皮亞諾存在性定理設 為 的一個開子集,以及一個連續函式:
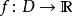 皮亞諾存在性定理
皮亞諾存在性定理 皮亞諾存在性定理
皮亞諾存在性定理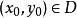 皮亞諾存在性定理
皮亞諾存在性定理皮亞諾存在定理:定義在 上的一個一階線性常微分方程(其中 )
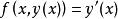 皮亞諾存在性定理
皮亞諾存在性定理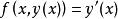 皮亞諾存在性定理
皮亞諾存在性定理 皮亞諾存在性定理
皮亞諾存在性定理 皮亞諾存在性定理
皮亞諾存在性定理必然有局部解。也就是說,必定存在一個關於 的鄰域 ,以及一個函式:
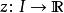 皮亞諾存在性定理
皮亞諾存在性定理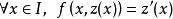 皮亞諾存在性定理
皮亞諾存在性定理滿足 。
相關定理
 皮亞諾存在性定理
皮亞諾存在性定理 皮亞諾存在性定理
皮亞諾存在性定理 皮亞諾存在性定理
皮亞諾存在性定理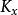 皮亞諾存在性定理
皮亞諾存在性定理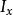 皮亞諾存在性定理
皮亞諾存在性定理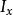 皮亞諾存在性定理
皮亞諾存在性定理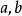 皮亞諾存在性定理
皮亞諾存在性定理皮亞諾存在定理可以和另外一個存在性定理:皮卡-林德洛夫定理作比較。相比起皮亞諾存在定理,皮卡-林德洛夫定理對函式 的要求更嚴格,但結論也更強。皮卡-林德洛夫定理要求函式 局部地滿足利普希茨條件,也就是說在任意一點 的附近,都有一個常數 和一個鄰域 ,使得對於 中任意的 兩點,都有:
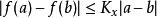 皮亞諾存在性定理
皮亞諾存在性定理。
這個要求比單純的連續性要高,但是得出的結論也更強了:皮卡-林德洛夫定理說明,在滿足上述要求時,微分方程的局部解不僅存在而且是唯一的。
例子
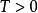 皮亞諾存在性定理
皮亞諾存在性定理設 為一個常數,考慮函式
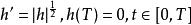 皮亞諾存在性定理
皮亞諾存在性定理。
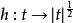 皮亞諾存在性定理
皮亞諾存在性定理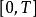 皮亞諾存在性定理
皮亞諾存在性定理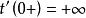 皮亞諾存在性定理
皮亞諾存在性定理 皮亞諾存在性定理
皮亞諾存在性定理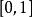 皮亞諾存在性定理
皮亞諾存在性定理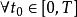 皮亞諾存在性定理
皮亞諾存在性定理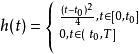 皮亞諾存在性定理
皮亞諾存在性定理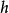 皮亞諾存在性定理
皮亞諾存在性定理 皮亞諾存在性定理
皮亞諾存在性定理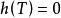 皮亞諾存在性定理
皮亞諾存在性定理根據皮亞諾存在定理,由於函式 在 上連續,微分方程有解。但由於 , 在 上不滿足利普希茨條件,於是解不一定是唯一的。事實上: ,函式都是微分方程的解,也就是說解有無窮多個。這個反例來源於一個物理模型:假設有一個漏水的容器,其水面高度(函式)和時間(變數)的關係由以上的微分方程定義的話,那么由於事實上可以觀測到漏水的過程,所以方程一定有解。但如果只知道容器在漏完水後的某個時刻的狀態()的話,是無法倒過來推測原來的水位有多高的(也就是說沒有唯一解)。
