介紹
通過疊代,可以發現有向一個單一點收縮和會聚的一個集合。在這種情況下,會聚到的這個點叫做吸引不動點。反過來說,疊代也可以表現得從一個單一點發散;這種情況叫不穩定不動點。
當軌道的點會聚於一個或多個極限的時候,軌道的會聚點的集合叫做極限集合或ω-極限集合。
吸引和排斥的想法類似推廣;依據在疊代下小鄰域行為,可把疊代分類為穩定集合和不穩定集合。
其他極限行為也有可能;比如,遊蕩點是總是移動永不回到甚至接近起點的點。
定義
 疊代函式
疊代函式在集合上的疊代函式的形式定義為:
 疊代函式
疊代函式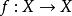 疊代函式
疊代函式 疊代函式
疊代函式 疊代函式
疊代函式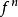 疊代函式
疊代函式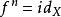 疊代函式
疊代函式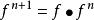 疊代函式
疊代函式 疊代函式
疊代函式設是集合和是函式。定義 的次疊代為而 ,這裡的是在 的恆等函式。
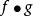 疊代函式
疊代函式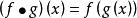 疊代函式
疊代函式在上述中, 指示函式複合;就是說。
從疊代建立序列
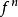 疊代函式
疊代函式 疊代函式
疊代函式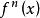 疊代函式
疊代函式 疊代函式
疊代函式函式的序列叫做 Picard 序列,得名於Charles Émile Picard。對於一個給定,的值的序列叫做的 軌道。
 疊代函式
疊代函式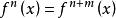 疊代函式
疊代函式 疊代函式
疊代函式 疊代函式
疊代函式 疊代函式
疊代函式如果對於某個整數有,則軌道叫做 周期軌道。對於給定最小的這種值叫做 軌道的周期。點自身叫周期點。
不動點
如果m=1,就是說如果對於某個 X中的 x有 f( x) = x,則 x被稱為疊代序列的 不動點。不動點的集合經常指示為 Fix( f)。存在一些不動點定理保證在各種情況下不動點的存在性,包括巴拿赫不動點定理和Brouwer不動點定理。
有很多技術通過不動點疊代產生了序列收斂加速。例如,套用於一個疊代不動點的Aitken方法叫做Steffensen方法,生成二次收斂。 不動點理論同樣也適用於經濟學領域。
極限行為
通過疊代,可以發現有向一個單一點收縮和會聚的一個集合。在這種情況下,會聚到的這個點叫做吸引不動點。反過來說,疊代也可以表現得從一個單一點發散;這種情況叫不穩定不動點。
當軌道的點會聚於一個或多個極限的時候,軌道的會聚點的集合叫做 極限集合或 ω-極限集合。
吸引和排斥的想法類似推廣;依據在疊代下小鄰域行為,可把疊代分類為穩定集合和不穩定集合。
其他極限行為也有可能;比如,遊蕩點是總是移動永不回到甚至接近起點的點。
例子
著名的疊代函式包括曼德博集合和疊代函式系統。
如果 f是一個群元素在一個集合上的作用,則疊代函式對應於自由群。

