概念
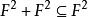畢達哥拉斯域
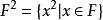畢達哥拉斯域畢達哥拉斯域(Pythagorean field)是一類重要的實域。一個實域F稱為是畢達哥拉斯域，是指： ，這裡 。即一個實域F是畢達哥拉斯域，若且唯若F是它的弱亞正錐。歐氏域、實閉域都是畢達哥拉斯域。畢達哥拉斯域的一個重要刻畫是：域F為畢達哥拉斯域，若且唯若-1∈F，且F沒有4次循環擴張。畢達哥拉斯域具有所謂的“下降”性質：畢達哥拉斯域F的任何一個滿足[F∶E]<∞的子域E也是畢達哥拉斯域。
域
設P是一至少含有兩個元素的環，如果在P中乘法還具有下列性質：
(1)有單位元素，即在P中有一元素e，使ea=ae=a，對所有的a∈P；
(2)有逆元素，即對p中每個非零元素a都有一元素a，使aa=aa=e；
(3)交換律成立，即ab=ba，a，b∈P，那么P就叫做一個域。域有下列的基本性質：
(1)域沒有零因子；
(2)若集F在兩個 二元運算(加法和乘法)下滿足下列條件，則F為一個域：
①F是以零為單位元的加法群；
②由除零外的F的一切元組成的集在乘法下是一個交換群；
③乘法對加法是可分配的；
(3)在域F中，方程ax=b(a，b∈F，a≠0)有唯一的解，並記作x=a/b；
(4)在F中，指數律成立；
(5)若把域F的單位元e的n倍ne記作n，則F中任一元a的n倍na就是n與a的積na。
實域
亦稱形式實域。是與序域密切相關的一種域。一個域F，若在其中不存在形式如：
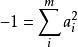畢達哥拉斯域的等式，此處a∈F，則稱F是實域(或者形式實域)。序域都是實域.反之，實域一定是可序域。因此，序域理論就是實域理論。實域理論是阿廷(Artin，E.)和施賴埃爾(Schreier，O.)於1926年首先建立的。阿廷在這一理論的基礎上，成功地正面解答了希爾伯特第17問題。實域理論又是近20年來蓬勃興起的實代數幾何的基礎。
亞正錐
含於正錐內的特殊子集。域F的子集T，若滿足下列條件：
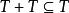畢達哥拉斯域1. ；
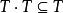畢達哥拉斯域2. ；
3.對每個a∈F，都有a∈T；
4.-1∉T；
則稱T為F的亞正錐。每個亞正錐都可以擴大成包含它的正錐；二者間的關係是：
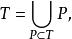畢達哥拉斯域即亞正錐T等於所有包含它的正錐P之交。在實域F中，由全部有限平方和組成的子集S是F的一個最小的亞正錐，稱為F的弱亞正錐。從上面列舉的事實得知，F的弱亞正錐是F中所有正錐的交。
人物簡介
畢達哥拉斯是古希臘哲學家、數學家，畢達哥拉斯學派的創始人。生於當時世界主要政治、經濟、文化中心之一的希臘薩摩斯島。青少年時就熱衷於研究學術和宗教儀式，曾去埃及、巴比倫和希臘各地遊歷，以博學聞名於世。曾在埃及居住10年左右，熟悉當地的宗教、種種具有宗教意義的禁忌、一切生物血緣相通靈魂不朽和輪迴的思想，以及算術、幾何學、天文學等。由於反對波呂克拉底(Polykrates)在薩摩斯島推行僭主政治，公元前529年，定居於古希臘在義大利南部的殖民城邦克羅頓島，招收門徒，建立具有神秘色彩的，合政治、宗教、哲學自然科學研究三者為一體的畢達哥拉斯學派盟會組織(習稱畢達哥拉斯同盟)，成為當地保守的貴族政治的決策核心。積極開展宗教活動，宣揚靈魂不朽和輪迴轉世，認為憑藉秘密入教儀式等就可以得到拯救。積極推進數學和自然科學的研究，以此作為淨化靈魂的重要途徑，並因此開創了一種嶄新而影響深遠的生活方式。通過研究數學進到本原的研究，認為數的本原就是萬物的本原，整個宇宙是由數產生的，是按數的原則構成的，是一個和諧的世界。人是一個和諧的“小宇宙”，是靈魂和肉體組成的整體。人的本性和道德都取決於靈魂。靈魂是推動自己的數，數的原則決定人的善惡和幸福。和諧是數的本性和原則。美德是一種和諧。他生前並無著作，但該學派有把所有著作和學說歸諸創始人的傳統，所以其本人學說和學派其他成員的學說難以區別。
