代數數論
代數數論是數論的一個重要分支,它以代數整數,或者代數數域為研究對象。不少整數問題的解決要藉助於或者歸結為代數整數的研究。因此,代數數論是整數研究的一個自然的發展。代數數論的發展也推動了代數學的發展。
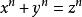 代數整數
代數整數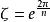 代數整數
代數整數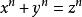 代數整數
代數整數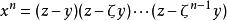 代數整數
代數整數代數數論主要起源於對費馬猜想的研究。費馬猜想(不定方程 (n>2)沒有xyz≠0的整數解)的證明可歸結為n=4及n為奇素數情形的證明。19世紀中葉,庫默爾試圖利用n次本原單位根ζ ,把方程 寫成 ,從而證明費馬猜想。但這需要有一個前提,即在分圓域Q(ζ)(添加單位根ζ到有理數域上生成的擴域)中,“整數”也像普通整數一樣,可以唯一地分解成素數的乘積。但在狄利克雷的啟發下,庫默爾發現分圓域中的“整數”分解成素因子的乘積不具有唯一性。庫默爾因此引入了“理想數”概念,每個“理想數”可以唯一地分解成素因子的乘積,這樣建立了分圓域上的數論。戴德金把庫默爾的工作系統化並推廣到一般的代數數域,奠定了代數數論的基礎。
高斯關於二次域的研究是代數數論的另一個重要起源。1801年,高斯發表的著名著作《算術研究》,展示了他的一個傑出的思想:把有理數域和有理整數環上的許多初等數論問題,放到更大的域和環一一二次域和它的代數整數環上來研究,這也導致了代數數論的開端。
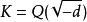 代數整數
代數整數代數數論也是活躍的數學前沿理論。一方面是對一些古典問題得出新的結果。例如,1801年高斯曾提出過兩個猜想:(1)只有有限多個類數為1的虛二次域;(2)存在無限多個類數為1的實二次域。關於(1),1934年,海布雷恩證明了當d(k)(k為有理數域的二次擴域,d(k)為k的判別式)→∞時,h(k的類數)→∞;1966年貝克,1967年斯塔克證明了類數為1的虛二次域 的虛二次域 只有9個:d=1,2,3,7,11,19,43,67,163。猜想(2)仍在研究之中。另一方面就是不斷開闢新的研究領域,如數域的阿貝爾擴張理論。1898—1899年間希爾伯特提出一個著名的猜想:希爾伯特類域猜想,1907年富特文格勒證明了這個猜想。韋伯對推廣希爾伯特類域做了大量工作,例如,推廣了理想類群的概念,得到一些全新的結果。1920年,高木貞治套用韋伯的理想類群概念,推廣了希爾伯特的結果,建立了完整的類域論。現在類域論已發展成為極其重要的、成果甚豐的數學領域。
代數數論的一大特點是,不僅由它可解決一系列整數規律問題,而且它的成果幾乎可以用到每一個數學領域中。
代數數
代數數是一類複數。即滿足代數方程的複數。是代數數論的基本研究對象之一。設α為複數,若存在係數為有理數的多項式f(x)使f(α)=0,則稱α為代數數。當f(x)在有理數域Q上不可約時,f(x)的次數稱為α的次數。添加代數數α到Q中得到域Q(α),稱為代數數域或數域。在有理數之外,歷史上第一個被發現的代數數是,它的發現曾引起畢達哥拉斯(Pythagoras)學派的驚恐。形如:
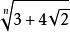 代數整數
代數整數等的根式均為代數數;但五次以上的代數數不一定再能用根式表出。不是代數數的複數稱為超越數,例如圓周率π.代數數的基本性質有:
1.全體代數數所成之集是一可數集.
2.兩個代數數之和、差、積、商(除數不為0)仍為代數數.
3.一個代數數的次數是惟一確定的.
4.係數為代數數的代數方程的根仍然是代數數.
整係數(或有理係數)代數方程的根。它是整數經加、減、乘、除以及開有限次方得到的數。
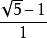 代數整數
代數整數例如, 是一個代數數,因為它滿足方程:x²+x-1=0。
一切用根式表示的數,都是代數數,但代數數不一定都能用根式表示,例如5次及5次以上代數方程的根,一般不能用根式表示。
代數整數概念
代數整數(algebraic integer),亦稱整數。代數數的一種。它是有理整數(即自然數、零及其相反數)的推廣。設α為複數,若存在係數為有理整數的首一(即最高次項係數為1)多項式f(x)使f(α)=0,則稱α為代數整數。若上述f(x)的常數項為±1,則α稱為單位。所有整數全體構成一個交換環I,其商域(或稱分式域)即為代數數全體構成的域A。單位即是環I中的可逆元素。代數整數的一個顯著特點是,它們不一定能進行惟一不可約因子分解。例如,
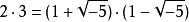 代數整數
代數整數由此導致理想概念的引入。整數的概念也被推廣到普通算術域F。若S是F的一個賦值集,S中賦值的賦值環之交集中元素稱為S整數。
代數整數性質
定義:如果α是一個有理數多項式:
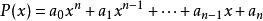 代數整數
代數整數的根,則稱α為一個代數數。若P(x)的係數都是整數,則稱α為一個代數整數。α所滿足的次數最低的多項式稱為α的極小多項式,極小多項式的次數稱為α的次數。
顯然,每個代數整數一定是代數數,反之不真實代數數與代數整數的極小多項式是唯一的。
定理1:一個有理數是代數整數若且唯若它是有理整數。
定理2:在通常的複數加法與乘法下,全體代數數構成一個域,全體代數整數構成一個環。
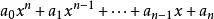 代數整數
代數整數 代數整數
代數整數 代數整數
代數整數定理3:假設α是多項式: 的根,如果 都是代數數,那么α一定是代數數;如果 都是代數整數,且a0=1,那么α一定是代數整數。
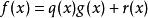 代數整數
代數整數定理4:如果f(x)與g(x)是域F上的兩個多項式,且g(x)≠0,那么存在唯一的q(x),r(x)∈F[x],使得: 。這裡r(x)=0,或者deg r(x)≤deg g(x)。
