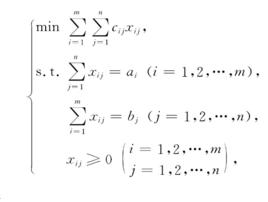基本介紹
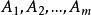 產銷平衡運輸問題
產銷平衡運輸問題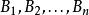 產銷平衡運輸問題
產銷平衡運輸問題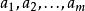 產銷平衡運輸問題
產銷平衡運輸問題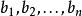 產銷平衡運輸問題
產銷平衡運輸問題設將某種物資從m個產地 運送到n個銷地 ,其中產量分別為 ,銷量分別為 ,並且
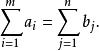 產銷平衡運輸問題
產銷平衡運輸問題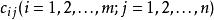 產銷平衡運輸問題
產銷平衡運輸問題已知從第i個產地到第j個銷地的每噸公里運費為 ,產銷平衡運輸問題就是要解決如何調運才能既滿足上述需要,又使總的運輸噸公里費用達到最少。
上面這些給定的數據通常用產銷平衡表和單位運價表表示 :
| 產銷平衡表 | 單位運價表 | ||
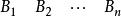 產銷平衡運輸問題 產銷平衡運輸問題 | 產量/噸 | 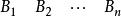 產銷平衡運輸問題 產銷平衡運輸問題 | |
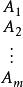 產銷平衡運輸問題 產銷平衡運輸問題 | 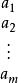 產銷平衡運輸問題 產銷平衡運輸問題 |  產銷平衡運輸問題 產銷平衡運輸問題 | |
| 銷量/噸 | 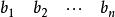 產銷平衡運輸問題 產銷平衡運輸問題 | ||
產銷平衡運輸問題的數學模型
產銷平衡運輸問題的數學模型為
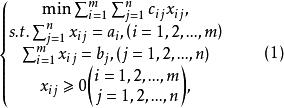 產銷平衡運輸問題
產銷平衡運輸問題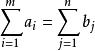 產銷平衡運輸問題
產銷平衡運輸問題其中,或用矩陣形式表示為
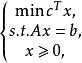 產銷平衡運輸問題
產銷平衡運輸問題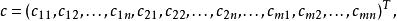 產銷平衡運輸問題
產銷平衡運輸問題其中
 產銷平衡運輸問題
產銷平衡運輸問題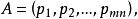 產銷平衡運輸問題
產銷平衡運輸問題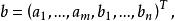 產銷平衡運輸問題
產銷平衡運輸問題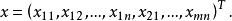 產銷平衡運輸問題
產銷平衡運輸問題A是一個結構特殊的稀疏矩陣,其特點如下:
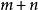 產銷平衡運輸問題
產銷平衡運輸問題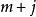 產銷平衡運輸問題
產銷平衡運輸問題(1)A有m*n列,每列有個元素,其中只有兩個為1,其餘元素為0,如P這兩個1所處位置為第i與第個分量。
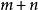 產銷平衡運輸問題
產銷平衡運輸問題(2)A有行,每行的特點為:前m行有n個1,這n個1連在一起,其餘元素為0;而後n行恰好是由m個n階單位矩陣並排在一起,即每行有m個1,每兩個1之間隔n-1個0元素,而且下一行的1往後錯一個位置 。
產銷平衡運輸問題數學模型的特點
運輸問題是一個特殊的線性規劃問題,線性規劃的理論對運輸問題也都是成立的。
此外,對於運輸問題,還有下面的特點。
定理1產銷平衡運輸問題式(1)必有可行解,也必有最優解。
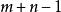 產銷平衡運輸問題
產銷平衡運輸問題定理2 產銷平衡運輸問題式(1)約束方程係數矩陣A的秩等於。
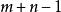 產銷平衡運輸問題
產銷平衡運輸問題定理3 運輸問題式(1)的基可行解中應包含個基變數 。