配送式配送運輸的方法
配送式配送運輸根據問題的性質不同有不同的求解方法,通常有圖上作業法、運輸問題的表上作業法、單純形法等等。(1)圖上作業法
圖上作業法是將貨物供需方的地理位置、交通情況、供貨量、需求量繪製成環線狀流向圖,根據就近分送的原則,進行簡便計算的貨物運輸規劃方法。如果交通網路圖為環狀線路,則要簡化為線狀線路,下面以環狀線路的步驟來說明求解方法。
1)求解步驟
①按各發運點、收貨點的地理位置,交通情況畫出環狀線路,並將各點相應的發貨量、運輸量和距離標上。(發點用框表示,收點用圈表示)
②甩掉里程最長的一段,使環狀線路變成線狀線路。
③按線狀線路的辦法安排調運,即按照已有線路進行就近分送,並在圖中用虛線表示,虛線通常畫在道路右側。
④計算配送行走線路的里圈長和外圈長,里圈長和外圈長均小於線路半圈長,則該配送線路為最優線路,否則不合理,要進行調整,調整思路為甩掉現有圈中運量較小的一段,補上原先甩去的那段,返回到③。
【例1】有三個發貨點A,B,C和五個收貨點D,E,F,G,H。其發貨量、收貨量和交通網路如圖所示,用圖上作業法求解配送線路。
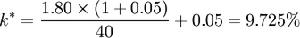
解 ①求初始解,甩去里程最長的一段BE,得線狀線路,按照就近分送的原則得到初始解,如圖所示。
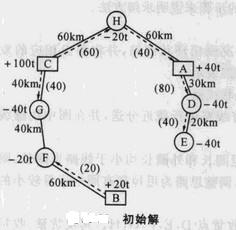
②解的檢驗:
半圈長:L/2=(30+20+80+60+40+40+60+60)/2=195km
里圈長:30+20+60+60+60=230km>195km
外圈長:40km<195km
所以初始解不合理,需要調整。
③恢復BE線路,甩去運量最小的線路BF,按就近分送原則得二次解,如圖所示。
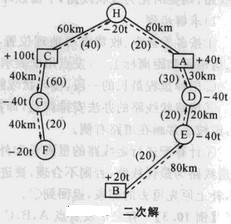
④解的檢驗:
里圈長:20+30+60+60=170km<195km
外圈長:80+40+40=160km<195km
則已得最優解。
(2)表上作業法
【例2】某部門有3個生產同類產品的工廠(產地),生產的產品由3個銷售點(銷地)出售,各工廠的生產量、各銷售點的銷售量(單位:萬噸)以及各工廠到各銷售點的單位運價(萬元/萬噸)如表1所示,要求研究產品如何調運才能使總運量最小?
產地 | B1 | B2 | B3 | 產量 | |
銷地 | |||||
A1 | 5 | 9 | 5 | 15 | |
A2 | 1 | 3 | 4 | 18 | |
A3 | 8 | 2 | 6 | 17 | |
銷量 | 18 | 12 | 16 | ||
解 該問題為產銷不平衡問題,因此應虛設一個銷地B4變為產銷平衡問題。
①求初始解:求初始解的方法通常有西北角法、最小元素法和沃格爾法,此處用沃格爾法求初始解,如表所示。
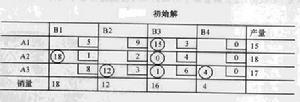
沃格爾法原理:計算出每一行及每一列中單位運價最小和次小的兩個元素之間的差值(稱行罰數或列罰數),再從差值最大的行或列中找出單位運價最小者,優先滿足其供銷關係,填一個數字用圈圈起來表示為基變數,並划去滿足供銷要求的行或列,直到所有供銷關係均滿足,即所有格均畫有線,基變數的個數為行和列數減去1。
②解的檢驗:解的檢驗方法通常有閉迴路法和位勢法(也稱對偶變數法)兩種,目的都是求出表中每個非基變數格(對應一個決策變數)的檢驗數,如果所有檢驗數全大於等於0,則為最優調運方案,否則要調整。在此用位勢法進行檢驗,如表所示。
因為所有非基變數檢驗數全大於0,則已得最優解。
運輸方案為:A1產地運往B3銷地15萬噸;A2產地運往B1銷地18萬噸;A3產地運往B2銷地12萬噸,B3銷地1萬噸。總運費為93萬元。
如果初始解檢驗不是最優解,則可用閉迴路法進行解的調整。
