定義
首先我們定義狄拉克代數的基矢，也就是16個狄拉克矩陣（實際上在4維情況下狄拉克矩陣有多種表示，但狄拉克代數的性質與其具體表示的選取無關） ：
狄拉克代數標量型矩陣：；
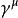狄拉克代數矢量型矩陣：，共4個；
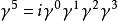狄拉克代數贗標量矩陣：；
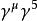狄拉克代數贗矢量矩陣：，共4個；
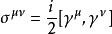狄拉克代數張量型矩陣：，共6個。
此外我們要求：
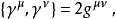狄拉克代數
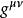狄拉克代數其中為洛倫茲度規，也具有不同的取法。
狄拉克代數 狄拉克代數 狄拉克代數通過如上定義，不難證明任一兩個狄拉克矩陣的乘積可以表達為這16個狄拉克矩陣的線性組合。我們設為任一一種狄拉克矩陣的線性組合（有時也直接管叫狄拉克矩陣），那么兩個任意矩陣的乘積也是16個狄拉克矩陣的線性組合。這樣我們就定義了一個關於加法、乘法都封閉的代數結構。
性質
加法滿足交換律、結合律、對數乘的分配律 ：
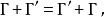狄拉克代數
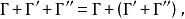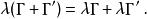狄拉克代數
狄拉克代數乘法滿足結合律、對加法的左、右分配律：
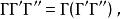狄拉克代數
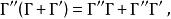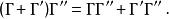狄拉克代數
狄拉克代數此外還有：
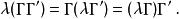狄拉克代數套用
狄拉克代數在描述狄拉克型費米子場時不可或缺，尤其是在構建諸如矢量流、贗矢流等的過程中。
標準模型中大部分的基本粒子是狄拉克型費米子，如夸克、輕子。它們的表述與相互作用的計算都離不開狄拉克代數。
此外在強子、介子衰變的研究中，也廣泛套用狄拉克代數。
