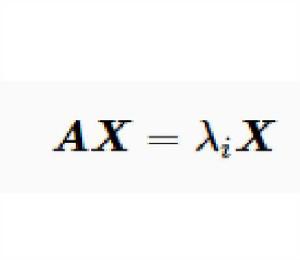定義
 特徵子空間
特徵子空間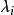 特徵子空間
特徵子空間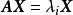 特徵子空間
特徵子空間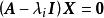 特徵子空間
特徵子空間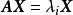 特徵子空間
特徵子空間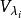 特徵子空間
特徵子空間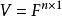 特徵子空間
特徵子空間 特徵子空間
特徵子空間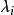 特徵子空間
特徵子空間方陣 的屬於特徵值 的特徵向量是齊次線性方程組 即 的非零解。此方程組 的解集 是 的子空間,稱為 的屬於特徵值 的 特徵子空間。
 特徵子空間
特徵子空間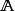 特徵子空間
特徵子空間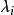 特徵子空間
特徵子空間線性空間 上線性變換 的屬於特徵值 :的全體特徵向量與零向量構成的集合。
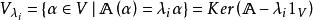 特徵子空間
特徵子空間 特徵子空間
特徵子空間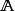 特徵子空間
特徵子空間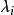 特徵子空間
特徵子空間是 的子空間,稱為 的屬於特徵值 的 特徵子空間。
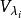 特徵子空間
特徵子空間只要求出了特徵子空間的 的一組基,基向量的全體非零線性組合就是全體特徵向量。
 特徵子空間
特徵子空間 特徵子空間
特徵子空間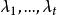 特徵子空間
特徵子空間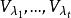 特徵子空間
特徵子空間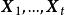 特徵子空間
特徵子空間同一線性變換 (或方陣 )的屬於不同特徵值 的特徵子空間之和是直和,屬於不同特徵值的特徵向量 線性無關。
對角化條件
 特徵子空間
特徵子空間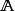 特徵子空間
特徵子空間 特徵子空間
特徵子空間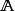 特徵子空間
特徵子空間上線性變換 如果在某組基下的矩陣 是對角陣,就稱 可對角化。
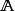 特徵子空間
特徵子空間 特徵子空間
特徵子空間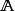 特徵子空間
特徵子空間 特徵子空間
特徵子空間 特徵子空間
特徵子空間在基M下的矩陣是對角陣 M的向量全部是 的特徵向量 各特徵子空間的直和等於 。
 特徵子空間
特徵子空間 特徵子空間
特徵子空間方陣 如果相似於對角陣,就稱 可對角化。
 特徵子空間
特徵子空間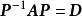 特徵子空間
特徵子空間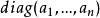 特徵子空間
特徵子空間 特徵子空間
特徵子空間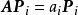 特徵子空間
特徵子空間是對角陣 P的各列是的特徵向量: 。
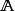 特徵子空間
特徵子空間 特徵子空間
特徵子空間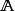 特徵子空間
特徵子空間可對角化 在任何一組基下的矩陣可對角化。
幾何重數與代數重數
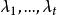 特徵子空間
特徵子空間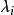 特徵子空間
特徵子空間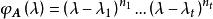 特徵子空間
特徵子空間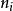 特徵子空間
特徵子空間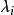 特徵子空間
特徵子空間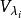 特徵子空間
特徵子空間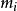 特徵子空間
特徵子空間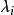 特徵子空間
特徵子空間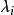 特徵子空間
特徵子空間設 是方陣 A的全部不同的特徵值,每個特徵值 在特徵多項式 中的重數 稱為 的 代數重數,特徵子空間 的維數 稱為 幾何重數,每個特徵值 的幾何重數≥1且≤代數重數。
 特徵子空間
特徵子空間 特徵子空間
特徵子空間可對角化 所有的特徵值的幾何重數等於代數重數。
 特徵子空間
特徵子空間 特徵子空間
特徵子空間特殊情形:如果n階方陣 有n個不同的特徵值,則每個特徵值的代數重數和幾何重數都等於1, 可對角化。
例題分析與解答
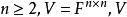 特徵子空間
特徵子空間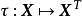 特徵子空間
特徵子空間 特徵子空間
特徵子空間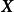 特徵子空間
特徵子空間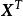 特徵子空間
特徵子空間 特徵子空間
特徵子空間 特徵子空間
特徵子空間設 的線性變換 將 中每個方陣 送到它的轉置 。求 的特徵值和特徵向量, 是否可對角化?
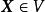 特徵子空間
特徵子空間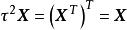 特徵子空間
特徵子空間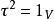 特徵子空間
特徵子空間 特徵子空間
特徵子空間 特徵子空間
特徵子空間 特徵子空間
特徵子空間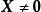 特徵子空間
特徵子空間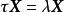 特徵子空間
特徵子空間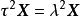 特徵子空間
特徵子空間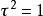 特徵子空間
特徵子空間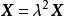 特徵子空間
特徵子空間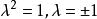 特徵子空間
特徵子空間解 對任意 有 ,可見 是 上的恆等變換, 的屬於每個特徵值 的特徵向量 滿足 從而 ,將 代入得 ,從而 。
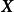 特徵子空間
特徵子空間 特徵子空間
特徵子空間 特徵子空間
特徵子空間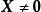 特徵子空間
特徵子空間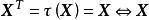 特徵子空間
特徵子空間是 的屬於特徵值1的特徵向量 且 是非零對稱方陣。
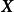 特徵子空間
特徵子空間 特徵子空間
特徵子空間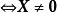 特徵子空間
特徵子空間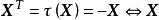 特徵子空間
特徵子空間是 的屬於特徵值-1的特徵向量 且 是非零斜對稱方陣。
 特徵子空間
特徵子空間存在一組由特徵向量組成的基:
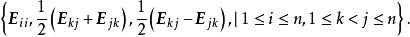 特徵子空間
特徵子空間 特徵子空間
特徵子空間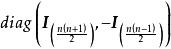 特徵子空間
特徵子空間在這組基下的矩陣是對角陣 。