概念
對於大型特徵值問題,要求其全部特徵值是非常困難的,一般情況下也無必要。如大型結構,其動力自由度可能成千上萬,往往只需要前10~20階自由振動頻率,這時候就可用子空間疊代法。實踐證明,子空間疊代法是求解大型特徵值問題前幾階特徵值最有效的方法之一。子空間疊代法的基本思想是逆疊代法和瑞利一里茲法(Rayleigh-Ritz)的結合。
子空間疊代法也稱同時疊代法,它是乘冪法的直接推廣,能同時求出模較大的一些特徵值和相應的特徵向量。與乘冪法的區別主要在兩個方面:第一,同時疊代法是同時用幾個(例如p個)線性無關的正交規範向量進行類似於乘冪法的疊代。若將選代向量看作一個p維子空間的(正交規範)基,則每疊代一次就得到一個新的子空間.第二,在疊代過程中套用Rayleigh-Ritz原理進行加速。因此,同時疊代法比乘冪法更便於進行自動計算,而且加快了收斂速度,它是目前求解大型、稀疏矩陣特徵值問題的最有效的方法之一。
基本原理
瑞利商
對於廣義特徵值問題
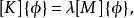 子空間疊代法
子空間疊代法定義任一矢量的瑞利商如下:
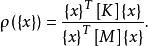 子空間疊代法
子空間疊代法瑞利商具有如下性質:
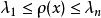 子空間疊代法
子空間疊代法① ;
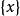 子空間疊代法
子空間疊代法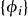 子空間疊代法
子空間疊代法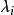 子空間疊代法
子空間疊代法②當 取特徵矢量 時,瑞利商達到駐值,這個駐值就是對應的特徵值 。
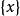 子空間疊代法
子空間疊代法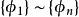 子空間疊代法
子空間疊代法證明:①將 用特徵向量 展開,即
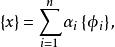 子空間疊代法
子空間疊代法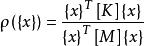 子空間疊代法
子空間疊代法將上式代入 式子中,並考慮特徵向量的正交性,有
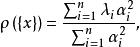 子空間疊代法
子空間疊代法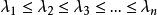 子空間疊代法
子空間疊代法由於 ,所以
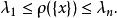 子空間疊代法
子空間疊代法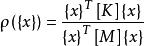 子空間疊代法
子空間疊代法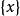 子空間疊代法
子空間疊代法②將 式子對 求導,得
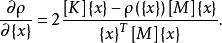 子空間疊代法
子空間疊代法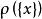 子空間疊代法
子空間疊代法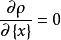 子空間疊代法
子空間疊代法取駐值時, ,即
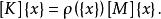 子空間疊代法
子空間疊代法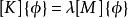 子空間疊代法
子空間疊代法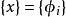 子空間疊代法
子空間疊代法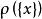 子空間疊代法
子空間疊代法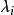 子空間疊代法
子空間疊代法比較上式和 式子可知,當 時, 取駐值,這個駐值就是 。
瑞利一里茲法
 子空間疊代法
子空間疊代法 子空間疊代法
子空間疊代法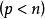 子空間疊代法
子空間疊代法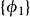 子空間疊代法
子空間疊代法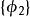 子空間疊代法
子空間疊代法 子空間疊代法
子空間疊代法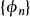 子空間疊代法
子空間疊代法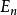 子空間疊代法
子空間疊代法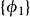 子空間疊代法
子空間疊代法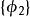 子空間疊代法
子空間疊代法 子空間疊代法
子空間疊代法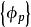 子空間疊代法
子空間疊代法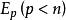 子空間疊代法
子空間疊代法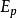 子空間疊代法
子空間疊代法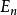 子空間疊代法
子空間疊代法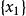 子空間疊代法
子空間疊代法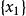 子空間疊代法
子空間疊代法 子空間疊代法
子空間疊代法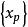 子空間疊代法
子空間疊代法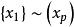 子空間疊代法
子空間疊代法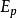 子空間疊代法
子空間疊代法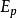 子空間疊代法
子空間疊代法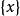 子空間疊代法
子空間疊代法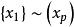 子空間疊代法
子空間疊代法用瑞利一里茲法,可以將 階廣義特徵值問題降為一個 階 廣義特徵值問題來求解。記 、 、 、 構成的空間為 , 、 、 、 構成的空間為 , 是全部特徵矢量空間 的一個子空間。任取一組線性無關的矢量 、 、 、 ,如果 是子空間 的一個基底,則 內的任一矢量 都可由 的線形組合表示:
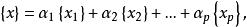 子空間疊代法
子空間疊代法即:
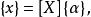 子空間疊代法
子空間疊代法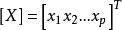 子空間疊代法
子空間疊代法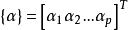 子空間疊代法
子空間疊代法其中 ; 。
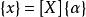 子空間疊代法
子空間疊代法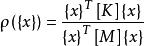 子空間疊代法
子空間疊代法將 代入 式子中,得:
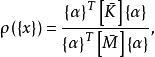 子空間疊代法
子空間疊代法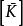 子空間疊代法
子空間疊代法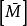 子空間疊代法
子空間疊代法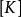 子空間疊代法
子空間疊代法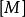 子空間疊代法
子空間疊代法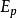 子空間疊代法
子空間疊代法其中 、 稱為 、 在子空間 內的投影,即:
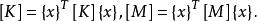 子空間疊代法
子空間疊代法由於
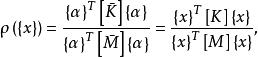 子空間疊代法
子空間疊代法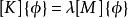 子空間疊代法
子空間疊代法 子空間疊代法
子空間疊代法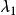 子空間疊代法
子空間疊代法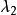 子空間疊代法
子空間疊代法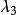 子空間疊代法
子空間疊代法 子空間疊代法
子空間疊代法 子空間疊代法
子空間疊代法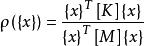 子空間疊代法
子空間疊代法 子空間疊代法
子空間疊代法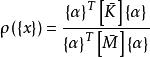 子空間疊代法
子空間疊代法 子空間疊代法
子空間疊代法所以,廣義特徵值問題的前個特徵值、、、、(式子的前個駐值),就是的個駐值。
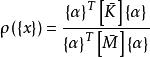 子空間疊代法
子空間疊代法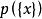 子空間疊代法
子空間疊代法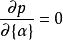 子空間疊代法
子空間疊代法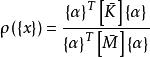 子空間疊代法
子空間疊代法通過對式子取的駐值,即,得到與式子等價的廣義特徵值問題:
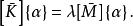 子空間疊代法
子空間疊代法 子空間疊代法
子空間疊代法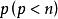 子空間疊代法
子空間疊代法這樣,就將階廣義特徵值問題轉化為階廣義特徵值問題,減小了問題的規模。

