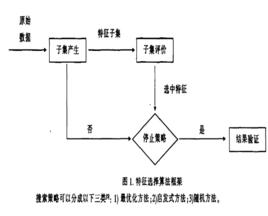
四要素
一般而言,特徵選擇可以看作一個搜尋尋優問題。對大小為n 的特徵集合, 搜尋空間由2n-1 種可能的狀態構成。Davies 等證明最小特徵子集的搜尋是一個NP 問題,即除了窮舉式搜尋,不能保證找到最優解。但實際套用中,當特徵數目較多的時候, 窮舉式搜尋因為計算量太大而無法套用,因此人們致力於用啟發式搜尋算法尋找次優解。一般特徵選擇算法必須確定以下4 個要素:1)搜尋起點和方向;2)搜尋策略;3)特徵評估函式;4)停止準則。
搜尋起點和方向
搜尋起點是算法開始搜尋的狀態點,搜尋方向是指評價的特徵子集產生的次序。搜尋的起點和搜尋方向是相關的,它們共同決定搜尋策略。一般的,根據不同的搜尋起點和方向,有以下4 種情況:
1)前向搜尋搜尋起點是空集S,依據某種評價標準,隨著搜尋的進行,從未被包含在S 里的特徵集中選擇最佳的特徵不斷加入S。
2)後向搜尋搜尋起點是全集S,依據某種評價標準不斷從S 中剔除最不重要的特徵,直到達到某種停止標準。
3)雙向搜尋雙向搜尋同時從前後兩個方向開始搜尋。一般搜尋到特徵子集空間的中部時,需要評價的子集將會急劇增加。當使用單向搜尋時,如果搜尋要通過子集空間的中部就會消耗掉大量的搜尋時間,所以雙向搜尋是比較常用的搜尋方法。
4)隨機搜尋隨機搜尋從任意的起點開始,對特徵的增加和刪除也有一定的隨機性。
搜尋策略
假設原始特徵集中有n 個特徵(也稱輸入變數),那么存在2 -1 個可能的非空特徵子集。搜尋策略就是為了從包含
2 -1 個候選解的搜尋空間中尋找最優特徵子集而採取的搜尋方法。搜尋策略可大致分為以下3 類:
1)窮舉式搜尋它可以搜尋到每個特徵子集。缺點是它會帶來巨大的計算開銷,尤其當特徵數較大時,計算時間很長。分支定界法(Branch and Bound, BB)通過剪枝處理縮短搜尋時間。
2)序列搜尋它避免了簡單的窮舉式搜尋,在搜尋過程中依據某種次序不斷向當前特徵子集中添加或剔除特徵,從而獲得最佳化特徵子集。比較典型的序列搜尋算法如:前向後向搜尋、浮動搜尋、雙向搜尋、序列向前和序列向後算法等。序列搜尋算法較容易實現,計算複雜度相對較小,但容易陷入局部最優。
3)隨機搜尋由隨機產生的某個候選特徵子集開始,依照一定的啟發式信息和規則逐步逼近全局最優解。例如:遺傳算法(Genetic Algorithm, GA)、模擬退火算法(SimulatedAnnealing, SA)、粒子群算法(Particl Swarm Optimization,PSO)和免疫算法(Immune Algorithm, IA)等。
特徵評估函式
評價標準在特徵選擇過程中扮演著重要的角色,它是特徵選擇的依據。評價標準可以分為兩種:一種是用於單獨地衡量每個特徵的預測能力的評價標準;另一種是用於評價某個特徵子集整體預測性能的評價標準。
在Filte方法中,一般不依賴具體的學習算法來評價特徵子集,而是借鑑統計學、資訊理論等多門學科的思想,根據數據集的內在特性來評價每個特徵的預測能力,從而找出排序較優的若干個特徵組成特徵子集。通常,此類方法認為最優特徵子集是由若干個預測能力較強的特徵組成的。相反,在Wrapper 方法中,用後續的學習算法嵌入到特徵選擇過程中,通過測試特徵子集在此算法上的預測性能來決定它的優劣,而極少關注特徵子集中每個特徵的預測性能如何。因此,第二種評價標準並不要求最優特徵子集中的每個特徵都是優秀的。
停止準則
停止標準決定什麼時候停止搜尋, 即結束算法的執行。它與評價準則或搜尋算法的選擇以及具體套用需求均有關聯。常見的停止準則一般有:
1)執行時間即事先規定了算法執行的時間,當到達所制定的時間就強制終止算法運行,並輸出結果。
2)評價次數即制定算法需要運算多少次,通常用於規定隨機搜尋的次數, 尤其當算法運行的結果不穩定的情況下,通過若干次的運行結果找出其中穩定的因素。
3) 設定閾值一般是給算法的目標值設定一個評價閾值,通過目標與該閾值的比較決定算法停止與否。不過,要設定一個合適的閾值並不容易,需要對算法的性能有十分清晰的了解。否則,設定閾值過高會使得算法陷入死循環,閾值過小則達不到預定的性能指標。
基本框架
 特徵選擇
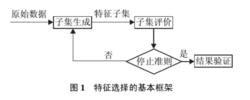
特徵選擇迄今為止, 已有很多學者從不同角度對特徵選擇進行過定義: Kira 等人定義理想情況下特徵選擇是尋找必要的、足以識別目標的最小特徵子集; John 等人從提高預測精度的角度定義特徵選擇是一個能夠增加分類精度, 或者在不降低分類精度的條件下降低特徵維數的過程; Koller 等人從分布的角度定義特徵選擇為: 在保證結果類分布儘可能與原始數據類分布相似的條件下, 選擇儘可能小的特徵子集;Dash 等人給出的定義是選擇儘量小的特徵子集, 並滿足不顯著降低分類精度和不顯著改變類分布兩個條件. 上述各種定義的出發點不同, 各有側重點, 但是目標都是尋找一個能夠有效識別目標的最小特徵子集. 由文獻可知, 對特徵選擇的定義基本都是從分類正確率以及類分布的角度考慮. Dash 等人給出了特徵選擇的基本框架, 如圖1 所示.
 特徵選擇
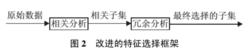
特徵選擇由於子集搜尋是一個比較費時的步驟, Yu 等人基於相關和冗餘分析, 給出了另一種特徵選擇框架, 避免了子集搜尋, 可以高效快速地尋找最優子集.框架如圖2 所示.
從特徵選擇的基本框架可以看出, 特徵選擇方法中有4 個基本步驟: 候選特徵子集的生成(搜尋策略)、評價準則、停止準則和驗證方法. 目前對特徵選擇方法的研究主要集中於搜尋策略和評價準則, 因而, 一般從搜尋策略和評價準則兩個角度對特徵選擇方法進行分類.
特徵選擇的一般過程
(1) 產生過程 ( Generation Procedure )
產生過程是搜尋特徵子集的過程,負責為評價函式提供特徵子集。
(2) 評價函式 ( Evaluation Function )
評價函式是評價一個特徵子集好壞程度的一個準則。
(3) 停止準則 ( Stopping Criterion )
停止準則是與評價函式相關的,一般是一個閾值,當評價函式值達到這個閾值後就可停止搜尋。
(4) 驗證過程 ( Validation Procedure )
在驗證數據集上驗證選出來的特徵子集的有效性。
基於搜尋策略的方法分類
基本的搜尋策略按照特徵子集的形成過程可分為以下3 種: 全局最優、隨機搜尋和啟發式搜尋. 一個具體的搜尋算法會採用兩種或多種基本搜尋策略,例如遺傳算法是一種隨機搜尋算法, 同時也是一種啟發式搜尋算法. 下面對3 種基本的搜尋策略進行分析比較.
1、採用全局最優搜尋策略的特徵選擇方法
迄今為止, 唯一得到最優結果的搜尋方法是分支定界法. 這種算法能保證在事先確定最佳化特徵子集中特徵數目的情況下, 找到相對於所設計的可分性判據而言的最優子集. 它的搜尋空間是O(2 ) (其中N 為特徵的維數). 存在的問題: 很難確定最佳化特徵子集的數目; 滿足單調性的可分性判據難以設計; 處理高維多類問題時, 算法的時間複雜度較高. 因此, 雖然全局最優搜尋策略能得到最優解, 但因為諸多因素限制, 無法被廣泛套用.
2、採用隨機搜尋策略的特徵選擇方法
在計算過程中把特徵選擇問題與模擬退火算法、禁忌搜尋算法、遺傳算法等, 或者僅僅是一個隨機重採樣過程結合起來, 以機率推理和採樣過程作為算法的基礎, 基於對分類估計的有效性, 在算法運行中對每個特徵賦予一定的權重; 然後根據用戶所定義的或自適應的閾值來對特徵重要性進行評價. 當特徵所對應的權重超出了這個閾值, 它便被選中作為重要的特徵來訓練分類器. Relief 系列算法即是一種典型的根據權重選擇特徵的隨機搜尋方法, 它能有效地去掉無關特徵, 但不能去除冗餘, 而且只能用於兩類分類. 隨機方法可以細分為完全隨機方法和機率隨機方法兩種. 雖然搜尋空間仍為O(2 ), 但是可以通過設定最大疊代次數限制搜尋空間小於O(2 ). 例如遺傳算法, 由於採用了啟發式搜尋策略, 它的搜尋空間遠遠小於O(2 ).存在的問題: 具有較高的不確定性, 只有當總循環次數較大時, 才可能找到較好的結果. 在隨機搜尋策略中, 可能需對一些參數進行設定, 參數選擇的合適與否對最終結果的好壞起著很大的作用. 因此, 參數選擇是一個關鍵步驟.
3、採用啟發式搜尋策略的特徵選擇方法
這類特徵選擇方法主要有: 單獨最優特徵組合,序列前向選擇方法(SFS), 廣義序列前向選擇方法(GSFS), 序列後向選擇方法(SBS), 廣義序列後向選擇方法(GSBS), 增l去r 選擇方法, 廣義增l去r選擇方法, 浮動搜尋方法. 這類方法易於實現且快速, 它的搜尋空間是O(N ). 一般認為採用浮動廣義後向選擇方法(FGSBS) 是較為有利於實際套用的一種特徵選擇搜尋策略, 它既考慮到特徵之間的統計相關性, 又用浮動方法保證算法運行的快速穩定性. 存在的問題是: 啟發式搜尋策略雖然效率高, 但是它以犧牲全局最優為代價.
每種搜尋策略都有各自的優缺點, 在實際套用過程中, 可以根據具體環境和準則函式來尋找一個最佳的平衡點. 例如, 如果特徵數較少, 可採用全局最優搜尋策略; 若不要求全局最優, 但要求計算速度快, 則可採用啟發式策略; 若需要高性能的子集, 而不介意計算時間, 則可採用隨機搜尋策略.
基於評價準則劃分特徵選擇方法
特徵選擇方法依據是否獨立於後續的學習算法, 可分為過濾式(Filter) 和封裝式(Wrapper)兩種.Filter 與後續學習算法無關, 一般直接利用所有訓練數據的統計性能評估特徵, 速度快, 但評估與後續學習算法的性能偏差較大. Wrapper 利用後續學習算法的訓練準確率評估特徵子集, 偏差小, 計算量大, 不適合大數據集. 下面分別對Filter 和Wrapper 方法進行分析.
1、過濾式(Filter) 評價策略的特徵選擇方法
Filter 特徵選擇方法一般使用評價準則來增強特徵與類的相關性, 削減特徵之間的相關性. 可將評價函式分成4 類: 距離度量、信息度量、依賴性度量以及一致性度量.
2、封裝式(Wrapper) 評價策略的特徵選擇方法
除了上述4 種準則, 分類錯誤率也是一種衡量所選特徵子集優劣的度量標準. Wrapper 模型將特徵選擇算法作為學習算法的一個組成部分, 並且直接使用分類性能作為特徵重要性程度的評價標準. 它的依據是選擇子集最終被用於構造分類模型. 因此, 若在構造分類模型時, 直接採用那些能取得較高分類性能的特徵即可, 從而獲得一個分類性能較高的分類模型. 該方法在速度上要比Filter 方法慢, 但是它所選擇的最佳化特徵子集的規模相對要小得多, 非常有利於關鍵特徵的辨識; 同時它的準確率比較高, 但泛化能力比較差, 時間複雜度較高. 目前此類方法是特徵選擇研究領域的熱點, 相關文獻也很多. 例如, Hsu 等人用決策樹來進行特徵選擇, 採用遺傳算法來尋找使得決策樹分類錯誤率最小的一組特徵子集. Chiang等人將Fisher 判別分析與遺傳算法相結合, 用來在化工故障過程中辨識關鍵變數, 取得了不錯的效果.Guyon 等人使用支持向量機的分類性能衡量特徵的重要性程度, 並最終構造一個分類性能較高的分類器. Krzysztof提出了一種基於相互關係的雙重策略的Wrapper 特徵選擇方法. 葉吉祥等人提出了一種快速的Wrapper 特徵選擇方法FFSR(fast featuresubset ranking), 以特徵子集作為評價單位, 以子集收斂能力作為評價標準. 戴平等人利用SVM線性核與多項式核函式的特性, 結合二進制PSO 方法, 提出了一種基於SVM的快速特徵選擇方法.
綜上所述, Filter 和Wrapper 特徵選擇方法各有優缺點. 將啟發式搜尋策略和分類器性能評價準則相結合來評價所選的特徵, 相對於使用隨機搜尋策略的方法, 節約了不少時間. Filter 和Wrapper 是兩種互補的模式, 兩者可以結合. 混合特徵選擇過程一般由兩個階段組成, 首先使用Filter 方法初步剔除大部分無關或噪聲特徵, 只保留少量特徵, 從而有效地減小後續搜尋過程的規模. 第2 階段將剩餘的特徵連同樣本數據作為輸入參數傳遞給Wrapper 選擇方法,以進一步最佳化選擇重要的特徵. 例如,有 文獻]採用混合模型選擇特徵子集, 先使用互信息度量標準和bootstrap 技術獲取前k個重要的特徵, 然後再使用支持向量機構造分類器.
研究進展及展望
自從上世紀90 年代以來, 特徵選擇得到廣泛研究並套用於Web 文檔處理(文本分類、文本檢索、文本恢復等)、基因分析、藥物診斷等領域。現在的社會是信息爆炸的社會, 越來越多、形式多樣的數據出現在我們面前, 比如基因數據、數據流, 如何設計出更好的特徵選擇算法來滿足社會的需求, 是一個長期的任務, 特徵選擇算法的研究在未來的一段時間仍將是機器學習等領域的研究熱點問題之一。目前研究熱點及趨勢主要集中於以下方面:
1) 特徵與樣本選擇的組合研究。不同的樣本集合區域, 也許應該選擇不同的特徵選擇算法。很多數據中存在特徵天然分割的特性, 如在網頁半監督分類問題中, 描述網頁特徵集( 一般為辭彙集) 通常可以分割為如下獨立的兩個特徵子集: 出現在網頁文本內容中的辭彙集合和出現在網頁的超級連結中的辭彙集合, 那么對於這兩個特徵子集, 我們能不能使用不同的特徵選擇方法來降低維數、取得更好的學習效果呢?
2)最近, 特徵及其與目標(分類、回歸、聚類等)的相關性受到越來越多的重視, 可以稱此問題為全相關間題。如在基因表達式分析中,找出所有特徵中那些和目標變數相關的特徵, 這些特徵可能導致生物狀態為健康或有疾病, 目前常用的是Ranking方法, 但Ranking方法往往考慮的是特徵和標籤的相關性, 沒有考慮特徵間的關聯,如何將特徵之間的關聯性考慮進去呢? 這也是目前研究的重點和難點之一。