定義
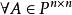 最小多項式
最小多項式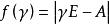 最小多項式
最小多項式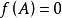 最小多項式
最小多項式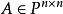 最小多項式
最小多項式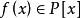 最小多項式
最小多項式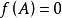 最小多項式
最小多項式 最小多項式
最小多項式由Cayley-Hamilton定理, , 是 A的特徵多項式,則 。因此,對任一矩陣 ,總可以找到一個多項式 ,使 。此時,也稱多項式 以A為根。
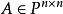 最小多項式
最小多項式設 ,在數域 P上的以 A為根的多項式中,次數最低的首項係數為1的那個多項式,稱為 A的最小多項式。
性質
① A的最小多項式是唯一的。
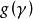 最小多項式
最小多項式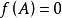 最小多項式
最小多項式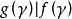 最小多項式
最小多項式②設是A的最小多項式,則等價於。
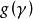 最小多項式
最小多項式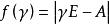 最小多項式
最小多項式③ A的最小多項式是它的特徵多項式的一個因式。
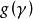 最小多項式
最小多項式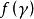 最小多項式
最小多項式④ A的最小多項式與它的特徵多項式在數域 P中有相同的根。
⑤相似的方陣陣具有相同的最小多項式。
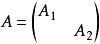 最小多項式
最小多項式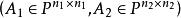 最小多項式
最小多項式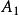 最小多項式
最小多項式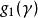 最小多項式
最小多項式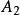 最小多項式
最小多項式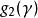 最小多項式
最小多項式⑥準對角矩陣的最小多項式等於的最小多項式與的最小多項式的最低公倍數。
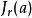 最小多項式
最小多項式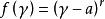 最小多項式
最小多項式⑦ r級 Jordan塊的最小多項式就是它的特徵多項式,也是它的初等因子。
套用
最小多項式的求解方法
方法一:
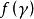 最小多項式
最小多項式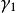 最小多項式
最小多項式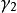 最小多項式
最小多項式 最小多項式
最小多項式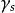 最小多項式
最小多項式(1)先將 A的特徵多項式在 P中作標準分解,找到A的全部特徵值,,,;
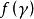 最小多項式
最小多項式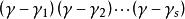 最小多項式
最小多項式(2)對的標準分解式中含有的因式按次數從低到高的順序進行檢測,第一個能零化A的多項式就是最小多項式。
方法二:
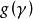 最小多項式
最小多項式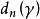 最小多項式
最小多項式設 A是n級複數矩陣,則A的最小多項式是A的最後一個不變因子。
例題
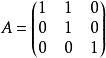 最小多項式
最小多項式求的最小多項式。
解: A的特徵多項式為:
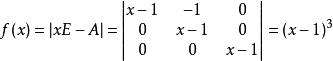 最小多項式
最小多項式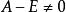 最小多項式
最小多項式又,
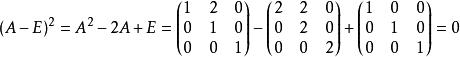 最小多項式
最小多項式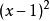 最小多項式
最小多項式故 A的最小多項式為。

