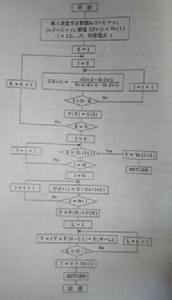
牛頓插值公式(Newton interpolation formula)是代數插值方法的一種形式。牛頓差值引入了差商的概念,使其在差值節點增加時便於計算。
差商
 牛頓插值公式
牛頓插值公式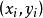 牛頓插值公式
牛頓插值公式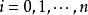 牛頓插值公式
牛頓插值公式設函式 ,已知其n+1個插值節點為 , ,我們定義:
 牛頓插值公式
牛頓插值公式 牛頓插值公式
牛頓插值公式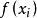 牛頓插值公式
牛頓插值公式在 的零階差商為 ;
 牛頓插值公式
牛頓插值公式 牛頓插值公式
牛頓插值公式 牛頓插值公式
牛頓插值公式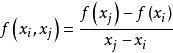 牛頓插值公式
牛頓插值公式在點 與 的一階差商為
 牛頓插值公式
牛頓插值公式 牛頓插值公式
牛頓插值公式 牛頓插值公式
牛頓插值公式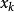 牛頓插值公式
牛頓插值公式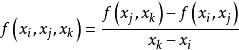 牛頓插值公式
牛頓插值公式在點 , , 的二階插商為
 牛頓插值公式
牛頓插值公式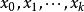 牛頓插值公式
牛頓插值公式一般的, 在點 的k 階差商為
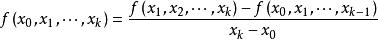 牛頓插值公式
牛頓插值公式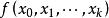 牛頓插值公式
牛頓插值公式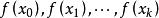 牛頓插值公式
牛頓插值公式可將k階差商 表示為函式值 的組合:
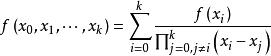 牛頓插值公式
牛頓插值公式公式推導
 牛頓插值公式
牛頓插值公式先寫出 的各階差商:
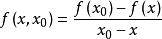 牛頓插值公式
牛頓插值公式;
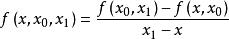 牛頓插值公式
牛頓插值公式;
 牛頓插值公式
牛頓插值公式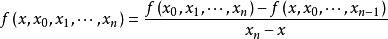 牛頓插值公式
牛頓插值公式分別變形可得:
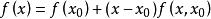 牛頓插值公式
牛頓插值公式;
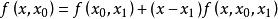 牛頓插值公式
牛頓插值公式;
 牛頓插值公式
牛頓插值公式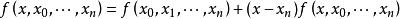 牛頓插值公式
牛頓插值公式依次代入,可得牛頓差值公式:
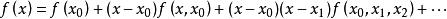 牛頓插值公式
牛頓插值公式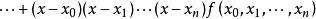 牛頓插值公式
牛頓插值公式可記為:
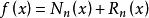 牛頓插值公式
牛頓插值公式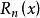 牛頓插值公式
牛頓插值公式其中,為牛頓差值公式的餘項或截斷誤差,當n趨於無窮大時為零。
等間距差值公式
取節點間距為h,可導出等間距牛頓差值公式。(以向前差分為例)
 牛頓插值公式
牛頓插值公式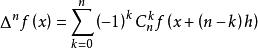 牛頓插值公式
牛頓插值公式的n 階向前差分公式為:
等間距牛頓差值公式:
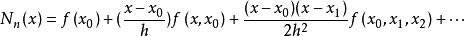 牛頓插值公式
牛頓插值公式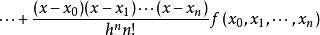 牛頓插值公式
牛頓插值公式實例
下圖為給定節點值利用牛頓差值擬合函式值得實例 :
 牛頓插值算例
牛頓插值算例公式意義
牛頓差值作為一種常用的數值擬合方法,因其計算簡單,方便進行大量差值點的計算,且邏輯清楚,便於編程計算,在實驗分析中具有廣泛的套用。
特別是實驗中經常出現只能測量得到離散數據點的情況,或者只能用數值解表示某對應關係之時,可以使用牛頓插值公式,對離散點進行擬合,得到較為準確的函式解析值。