基本介紹
 反插值
反插值 反插值
反插值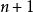 反插值
反插值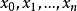 反插值
反插值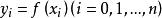 反插值
反插值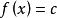 反插值
反插值 反插值
反插值 反插值
反插值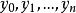 反插值
反插值 反插值
反插值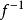 反插值
反插值反插值(inverse interpolation)是一種插值法,指利用插值函式反求滿足某條件之自變數的近似值。設給定函式在個不同點上的值,欲求使之的近似值,這裡是含的區間[α,β]中之某個值。反插值就是求的反函式在c處的近似值 。
方法步驟
 反插值
反插值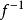 反插值
反插值 反插值
反插值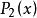 反插值
反插值 反插值
反插值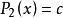 反插值
反插值 反插值
反插值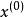 反插值
反插值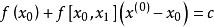 反插值
反插值求的反函式在c處的近似值通常可由的 牛頓插值公式,近似代替,再令,求出的近似,一般用逐次逼近法,先取使得滿足,即
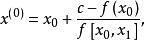 反插值
反插值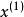 反插值
反插值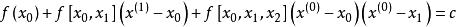 反插值
反插值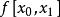 反插值
反插值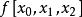 反插值
反插值 反插值
反插值再求,使它滿足,這裡及為的一階與二階均差。由上式得到
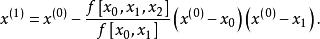 反插值
反插值然後用疊代公式
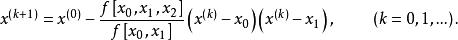 反插值
反插值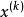 反插值
反插值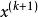 反插值
反插值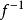 反插值
反插值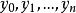 反插值
反插值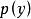 反插值
反插值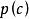 反插值
反插值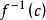 反插值
反插值疊代至與在所要求精度下相等為止。也可直接利用反函式以為節點的牛頓插值多項式,用近似。
反插值及餘項
 反插值
反插值假設函式以表格形式給出如下:
 反插值 反插值 |  反插值 反插值 |  反插值 反插值 |  反插值 反插值 | 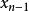 反插值 反插值 | 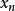 反插值 反插值 |
 反插值 反插值 | 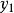 反插值 反插值 | 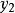 反插值 反插值 |  反插值 反插值 | 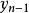 反插值 反插值 | 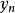 反插值 反插值 |
 反插值
反插值 反插值
反插值反插值就是要以函式的值來求自變數的的值。
 反插值
反插值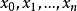 反插值
反插值 反插值
反插值 反插值
反插值 反插值
反插值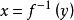 反插值
反插值設函式在含的區間上嚴格單調,則由高等數學知識可知,與是一一對應的,即存在反函式,此時反插值問題有唯一解存在 。
 反插值
反插值 反插值
反插值一般情況下,可用 拉格朗日插值多項式或 牛頓插值多項式,只須將與的位置互換即可。如用拉格朗日插值多項式對上表作反插值有
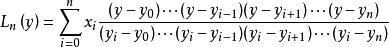 反插值
反插值反插值的餘項為
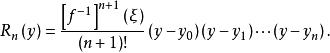 反插值
反插值