梯形法則
梯形法則是:
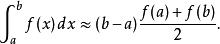 牛頓-柯特斯公式
牛頓-柯特斯公式這等同將被積函式近似為直線函式,被積的部分近似為梯形。
要求得較準確的數值,可以將要求積的區間分成多個小區間,再個別估計,即:
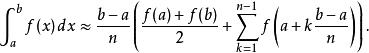 牛頓-柯特斯公式
牛頓-柯特斯公式可改寫成
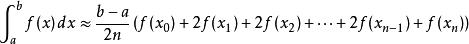 牛頓-柯特斯公式
牛頓-柯特斯公式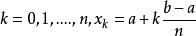 牛頓-柯特斯公式
牛頓-柯特斯公式其中對
辛普森法則
辛普森法則(Simpson's rule,又稱 森遜法則、 辛普森法則)是:
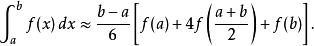 牛頓-柯特斯公式
牛頓-柯特斯公式同樣地,辛普森法則也有多重的版本:
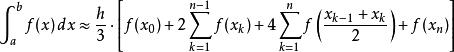 牛頓-柯特斯公式
牛頓-柯特斯公式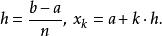 牛頓-柯特斯公式
牛頓-柯特斯公式或寫成
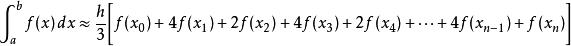 牛頓-柯特斯公式
牛頓-柯特斯公式牛頓-柯特斯公式
牛頓-柯特斯公式(Newton-Cotes rule / Newton-Cotes formula)以Roger Cotes和艾薩克·牛頓命名。其內容是:
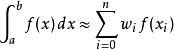 牛頓-柯特斯公式
牛頓-柯特斯公式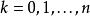 牛頓-柯特斯公式
牛頓-柯特斯公式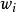 牛頓-柯特斯公式
牛頓-柯特斯公式 牛頓-柯特斯公式
牛頓-柯特斯公式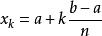 牛頓-柯特斯公式
牛頓-柯特斯公式其中 , 是常數(由 的值決定), 。
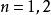 牛頓-柯特斯公式
牛頓-柯特斯公式梯形法則和辛普森法則便是 的情況。
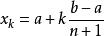 牛頓-柯特斯公式
牛頓-柯特斯公式亦有不採用在邊界點來估計的版本,即取 。
原理
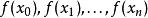 牛頓-柯特斯公式
牛頓-柯特斯公式假設已知的值。
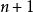 牛頓-柯特斯公式
牛頓-柯特斯公式 牛頓-柯特斯公式
牛頓-柯特斯公式以點進行插值,求得對應的拉格朗日多項式。
 牛頓-柯特斯公式
牛頓-柯特斯公式對該次的多項式求積。
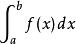 牛頓-柯特斯公式
牛頓-柯特斯公式 牛頓-柯特斯公式
牛頓-柯特斯公式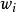 牛頓-柯特斯公式
牛頓-柯特斯公式該積分便可以作為的近似,而由於該拉格朗日多項式的係數都是常數(由決定其值),所以積函式的係數(即)都是常數。
缺點
對於次數較高的多項式而有很大誤差(龍格現象),不如高斯積分法。
