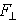無窮邏輯
正文
將一階邏輯中的公式和推理的長度推廣至無窮長得到的。在它的公式中，可以出現無窮多個公式的合取式或析取式，也可以出現無窮多個量詞。由於一階邏輯的模型論套用到數學的其他分支時受到了一定的限制，因而產生了無窮邏輯的模型理論。在描述集合論中也使用這種邏輯。1963年前後，因C.卡普及D.S.斯科特等的工作而發展起來，在1969年前後，J.巴威斯及M.馬凱依等又在這個方向上作出了重要的貢獻。如果α、β是兩個無窮基數(見集合論)，那么無窮邏輯Lαβ的形式語言與一階邏輯的形式語言相似,即除了有α個變元，可以在基數小於α的公式集上構作合取式或析取式,以及允許在小於β個變元上加全稱量詞或存在量詞外,結構與一階邏輯相同。因此,L
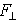就是通常的一階邏輯,另一簡單情形是L
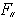。它的公式中允許出現可數無窮個公式的合取式或析取式，但只能出現有窮個量詞。例如，可用L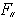的一個句子表示撓群的公理凬x∨｛n·x=0:0<n<ω｝；又如,全體有窮模型的類的特徵可以表示為
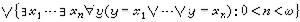等。 因為無窮邏輯L
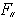套用最廣泛，且對它的研究也最深入，因此以L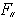為例，敘述無窮邏輯的一些主要結果。 可以用L
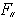邏輯的一個句子刻畫可數模型的全部性質，也就是說,如果L是一個只有可數個符號的語言，M是L的一個可數模型,那么存在L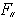中的一個句子φ,使得對於L的所有可數模型N，N≌M的必要且充分條件是N|=φ。此定理是斯科特於1965年證明的。 為保持L
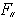邏輯的完備性，必須引進無窮長的推理規則，並且將形式證明的長度也推廣至無窮。 關於L
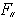的公理和推理規則上加上諸如公理:∧φ→φ，對於每個公式φ∈φ；推理規則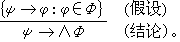 
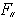中公式的可數集合。容易看出，上述的公理及推理規則的長度可以是無窮的。無窮邏輯的形式證明的定義同一階邏輯。易知，L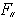的形式證明的長度必小於ω1（即為可數無窮）。 有了上述概念，就可以陳述關於L
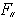的完備性定理（卡普，1964）:一個L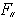中的句子φ是定理，若且唯若它是有效的。 假定L中僅有可數個符號,那么在L
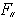中經常遇到的困難是它的公式集是不可數的。而在套用中常常只需考慮可數個公式就夠了。因此需要對L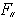的句子集（也記為L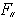）加以限制，建立起滿足一定性質的可數的公式子集的概念。如果用 A表示滿足一定性質的可數集合，則
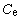稱為L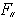上的一個斷片。 無窮邏輯L
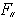失去了一階邏輯的兩個基本性質：緊緻性定理及勒文海姆－斯科朗－塔爾斯基定理。為了在L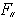的公式集的子集上建立緊緻性，引進了可允許集的概念。當A為可允許集時,LA就稱為可允許斷片,巴威斯在L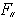的可允許斷片 LA上建立了相應於通常一階邏輯的緊緻性定理(1969)。 參考書目
J.Barwise,ed.,Hαndbook of Mαthemαticαl Logic,North-Holland, Amsterdam,1977.
H.J.Keisler,Model Theory for Infinitαry Logic,North-Holland,Amsterdam,1971.
