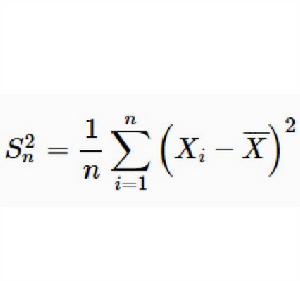定義
漸近無偏估計量是隨著樣本容量n增加趨於無偏的參數估計量。
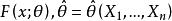漸近無偏估計量
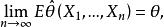漸近無偏估計量
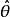漸近無偏估計量
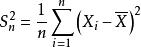漸近無偏估計量
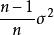漸近無偏估計量設總體X的分布函式為 是未知參數θ的一個估計量，若 則稱 是θ的 漸近無偏估計。如樣本方差 是總體方差的 漸近無偏估計，但並非無偏估計，因為它的數學期望為 。
無偏性與漸近無偏估計量
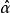漸近無偏估計量由於樣本的隨機性，對於個別樣本，其估計值可能偏大或偏小。但從平均值來看，一個好的估計量應該等於被估計參數。即 作為一個隨機變數，它所取的值應集中在未知參數的真值或均值附近。
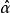漸近無偏估計量
漸近無偏估計量如果估計量 的均值(數學期望)等於被估計參量 (一般為隨機變數)的均值(數學期望)，則稱此估計量具有 無偏性，為 無偏估計量，數學表達式為
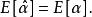漸近無偏估計量 漸近無偏估計量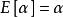
漸近無偏估計量若被估計參量 為確定的，即 ，則無偏性可表示為
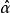漸近無偏估計量
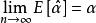漸近無偏估計量 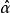漸近無偏估計量若 滿足關係式 (其中n 為樣本數)，則稱 為 漸近無偏估計量。
無偏性是一個所期望的性能。但一般情況下，漸近無偏估計量也是非常有用的。
例題分析
現在來考慮一個線性平穩過程的自相關函式的兩種估計量。
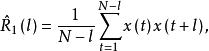漸近無偏估計量
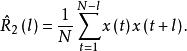漸近無偏估計量
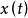漸近無偏估計量
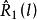漸近無偏估計量
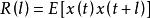漸近無偏估計量
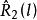漸近無偏估計量
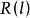漸近無偏估計量假定數據 是獨立觀測的，容易看出， 是 的一個無偏估計量，而 是 的有偏估計量，因為
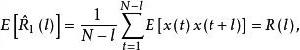漸近無偏估計量
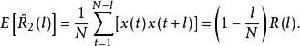漸近無偏估計量 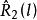漸近無偏估計量可以看到 是有偏的，但它是漸進無偏的，即
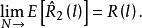漸近無偏估計量
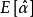漸近無偏估計量
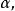漸近無偏估計量 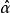漸近無偏估計量
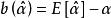漸近無偏估計量若 不等於 則稱 為有偏估計量，差值 稱為估計量的偏差或偏量。
估計量的無偏性保證了估計值分布在被估計量的真值或均值附近。
